Введение

Среди множества популярных алгоритмов на графах существует целый ряд алгоритмов, позволяющих находить кратчайшие пути. Каждый из них решает собственную задачу и, соответственно, имеет свое применение на практике. Так, например, алгоритм A* может использовать различные эвристики, чтобы находить путь минимальной стоимости в видеоиграх, а алгоритм Флойда — Уоршелла позволяет эффективно находить кратчайшие пути между всеми парами вершин в плотных графах и даже может использоваться в методе Шульца для определения победителя выборов [1]. Однако, одной из областей, в которых алгоритмы поиска кратчайших путей получили наибольшие развитие и применение, являются компьютерные коммуникационные сети.

В процессе разработки одной из таких систем перед нами встала задача организации динамической маршрутизации в сети с двухуровневой топологией. Как у большинства компаний, предоставляющих геораспределенные сервисы в Интернете, инфраструктура сети Qrator представлена в виде набора площадок, где каждая площадка представляет из себя набор вычислительных узлов в пределах одного дата-центра. Одной из задач разрабатываемой системы являлось выполнение операции AllReduce, заключающейся в применении операции редукции к изменяющимся во времени значениям на узлах. С ее помощью на каждом из узлов, например, можно было бы иметь представление о суммарном количестве трафика, обрабатываемом во всей сети. Основными целями при проектировании системы было, говоря неформально, снижение стоимости и увеличение качества передачи данных между узлами разных площадок.¹ Важной особенностью при решении задачи являлось то, что в результате широкого применения в Интернете ECMP-маршрутизации (маршрут выбирается, исходя из значения хэша от адресов источника и получателя пакета), качество связи между узлом \(a_1\) площадки \(A\) и узлом \(b_1\) площадки \(B\) могло существенно отличаться от качества связи между узлами \(a_2\) и \(b_2\) тех же площадок. Поэтому для оптимизации процесса обмена результатами промежуточных редукций между узлами мы решили реализовать собственный алгоритм динамической маршрутизации на уровне узлов. Нам стало интересно, как стандартные алгоритмы на графах применяются для подобных задач в реальных распределенных системах. В итоге мы довольно глубоко изучили теоретическую составляющую вопроса, и теперь готовы рассказать, как алгоритмы Дейкстры и Форда — Беллмана используются в этой области.

1   Задача динамической маршрутизации

Сперва напомним, в чем состоит задача динамической маршрутизации и какими особенностями она обладает.

Во всех современных сетях для обмена данными используется коммутация пакетов. При создании протокола динамической маршрутизации естественным являлось бы желание достигнуть такой работы алгоритма, чтобы каждый отдельный пакет проходил по некоторому  «наилучшему» маршруту. Почти всегда это сводится к задаче выбора такого соседа, через которого проходит хотя бы один из таких  «наилучших» путей до узла назначения — используется принцип динамического программирования в чистом виде. Такого соседа зачастую также называют next hop. Для удобства все актуальные next hop хранят в так называемой таблице маршрутизации, в которой каждому объекту назначения в соответствие ставится последний выбранный next hop. Таблицу маршрутизации можно обновлять в фоне независимо от работы приложений, использующих общение по сети: в момент отправки пакета достаточно взглянуть на таблицу маршрутизации, чтобы понять, какой из соседних узлов на данный момент является наиболее подходящим для дальнейшей передачи сообщения.

Возникает естественный вопрос: как сравнивать маршруты между собой для того, чтобы определить наилучший? Для этой цели заводится понятие метрики (веса, стоимости) отдельных каналов связи — ее значение может зависеть как от их статических (приоритет, пропускная способность канала, реальная стоимость передачи данных по нему), так и от динамических (RTT, процент потерь) показателей. В этой статье мы абстрагируемся от явного вида функции метрики и будем считать, что все узлы способны ее вычислить в текущий момент времени. Метрикой маршрута будем называть сумму метрик соединений между последовательными парами входящих в него узлов.

Итого, при построении маршрутизации нужно учитывать следующие 2 особенности:

1. Каждый узел системы решает свою локальную задачу: ему необходимо выбрать соседа, которому он должен передать данные, чтобы они в конце концов были доставлены до объекта назначения. Узлу \(a\) не интересно знать кратчайший путь между узлами \(b\) и \(c\), если он знает кратчайшие пути до каждого из них. Поэтому не все алгоритмы на графах в данной области применимы. Например, алгоритм Флойда — Уоршелла, который находит кратчайшие пути между всеми парами вершин в графе, тратит на это дополнительное время (суммарная сложность данного алгоритма \(O(V^3)\)), поэтому нет смысла использовать его в данной задаче.

2. Изменчивый характер системы и в частности каналов связи ограничивает набор гарантий, который может предоставить любой протокол динамической маршрутизации. Предположим, что узел \(s\) должен выбрать next hop из двух своих соседей \(a\) и \(b\) для передачи пакета до объекта назначения \(T\). Предположим, минимальный по метрике маршрут на данный момент проходит через узел \(a\). За ограниченное время узел \(s\) должен принять окончательное решение и приступить к отправке. Если бы мы хотели добиться от алгоритма гарантии того, что пакет пройдет по маршруту с наименьшей метрикой, в качестве next hop должен был быть выбран узел \(a\). Непосредственно после этого момента качество сети может измениться таким образом, что суммарные метрики всех маршрутов, проходящих через узел \(a\), станут больше суммарной метрики некоторого маршрута, проходящего через \(b\), и отправка произойдет неоптимальным образом. Поэтому наилучшей гарантией, которой мы можем добиться, является выбор минимальных по метрике маршрутов за ограниченное время после фиксирования метрик отдельных каналов связи.

2   Алгоритм Дейкстры и OSPF

Алгоритм Дейкстры является, пожалуй, самым популярным алгоритмом поиска кратчайших путей в графе. Существует множество ресурсов, на которых он подробно описывается и доказывается его корректность, поэтому мы лишь сошлемся на один из них. Если не вдаваться в подробности, в алгоритме все вершины последовательно добавляются в множество вершин \(U\), до которых веса кратчайших путей вычислены. Изначально множество \(U\) пусто, а все вершины хранятся в куче по минимуму со значениями, равными оценкам длин кратчайших путей до них. В процессе работы происходит последовательная релаксация ребер, исходящих из минимального элемента кучи: соответствующие смежные вершины проталкиваются по куче вверх, если был найден более короткий путь через релаксируемое ребро, а сама вершина из кучи добавляется в множество \(U\).

Важным аспектом данного алгоритма является то, что узел, на котором он запускается, должен иметь полное представление о топологии сети (графа). В таком виде ему нашли применение в современном протоколе динамической маршрутизации OSPF [2]. В этом протоколе вся автономная система (часть глобальной сети, в которой осуществляется маршрутизация) делится на зоны. Каждый маршрутизатор поддерживает базу данных состояния каналов (LSDB) между объектами его зоны и в случае ее изменения запускает алгоритм Дейкстры с обновленной информацией. Таким образом, если считать, что механизм флудинга в OSPF работает правильно, то корректность построения таблиц маршрутизации до объектов в пределах зоны сводится к корректности алгоритма Дейкстры. Более подробно про взаимодействие маршрутизаторов в OSPF можно почитать в этой статье.

OSPF является ярким примером подхода к решению задачи динамической маршрутизации под названием Link State. При его использовании узлы обмениваются информацией о состоянии отдельных каналов сети, что позволяет каждому из узлов иметь полное представление о текущей топологии. Это также позволяет сравнительно быстро узнавать о неполадках в отдаленных частях сети и сразу же на них реагировать.

Однако одной зоной автономная система не ограничивается, поэтому необходим дополнительный механизм, по которому будут строиться маршруты и во внешние зоны. В OSPF такой механизм есть: маршрутизаторы, находящиеся на границе зоны, анонсируют во внешнюю зону информацию об известных маршрутах в виде записей с суммарными метриками. За счет таких сообщений маршрутизаторы могут строить маршруты и до объектов, находящихся за пределами их зоны. Такой подход называется Distance Vector, и именно с ним наиболее тесно связан алгоритм Форда — Беллмана.

3   Алгоритм Форда — Беллмана и дистанционно-векторный подход

Здесь начинается наиболее интересная часть статьи. Для дальнейшего изложения нам понадобится четкое понимание принципа работы классического алгоритма Форда — Беллмана, поэтому мы опишем его самостоятельно.

Пусть во взвешенном графе \(G = (V, E)\) нам необходимо найти кратчайшие пути от вершины \(1\) до всех других вершин. Будем считать, что \(|V| = n\). Обозначим за \(d_i^{(k)}\) длину кратчайшего пути до вершины \(i\), найденного на \(k\)-ом шаге алгоритма. Начальная инициализация:

\[\tag{1} \begin{array}{c} d_i^{(0)} = + \infty,\ i \neq 1, \\ d_1^{(0)} = 0. \end{array}\]

На каждом шаге алгоритма мы насчитываем очередной набор значений \(d_i^{(k + 1)}\), \(i \neq 1\):

\[\tag{2} d_i^{(k + 1)} = \displaystyle \min_{j \in V,\ (j, i) \in E} \big(d_j^{(k)} + \omega(j, i)\big),\]

\(\omega(j, i)\) — вес ребра \((j, i)\). С помощью метода математической индукции по \(k\) можно показать, что при таком алгоритме значение \(d_i^{(k)}\) будет равно длине кратчайшего пути из вершины \(1\) в вершину \(i\), содержащего не более \(k\) ребер. Таким образом, не позже чем через \(n - 1\) итерацию алгоритма мы определим кратчайшие пути до каждой вершины, и с некоторого момента значения \(d_i^{(k)}\) перестанут изменяться. Отсюда несложно вычисляется и его сложность: на каждой итерации алгоритма мы пытаемся прорелаксировать все ребра, поэтому суммарное время работы составит \(O(|V| \cdot |E|)\).

Перейдем к описанию распределенного асинхронного алгоритма Форда — Беллмана. При использовании дистанционно-векторного подхода задачи маршрутизации до различных узлов решаются независимо друг от друга, а в работе алгоритма используется информация от соседних узлов. Чтобы отразить изменения в постановке задачи, введем новые обозначения: без ограничения общности за \(D_i\) примем длину кратчайшего пути от вершины \(i\) до вершины \(1\). Заметим, что этот набор значений является решением системы уравнений вида:

\[\tag{3} \begin{cases} D_i = \displaystyle \min_{j \in V,\ (i, j) \in E} \big(\omega(i, j) + D_j\big) &,\ i \neq 1 \\ D_1 = 0. \end{cases}\]

Можно заметить, что последовательность по \(k\) из наборов значений \(\{d_i^{(k)}\}_{i = 1}^n\) в процессе работы стандартного алгоритма Форда — Беллмана (2) стабилизируется к набору значений, являющимся решением системы уравнений, похожих на (3). Единственное отличие в уравнениях — направление ребер, что неудивительно, ведь в одном случае мы считаем длины путей от вершины \(1\), а в другом — до нее. Напомним, что алгоритм динамической маршрутизации запускается на каждом узле сети, и каждый из них строит собственную таблицу маршрутизации, содержащую оценки суммарных метрик наилучших маршрутов до различных объектов назначения. В частности, каждый узел \(i\) может поддерживать собственную оценку \(D_i(t)\) значения \(D_i\). Будем также считать, что соединения в нашей сети двунаправленные: \((i, j) \in E \iff (j, i) \in E\), а значит соседние узлы могут обмениваться оценками \(D_i(t)\) и \(D_j(t)\) между собой. Таким образом, все узлы системы, получив оценки от своих соседей, смогут провести итерацию алгоритма Форда — Беллмана вида (3). При доказательстве корректности стандартного алгоритма Форда — Беллмана (2) мы уже показали, что с начальными условиями (1) при фиксированных значениях метрик каналов связи за конечное количество итераций оценки \(D_i(t)\) стабилизируются и становятся равны \(D_i\). Однако тут возникает сразу две проблемы: 1) синхронное выполнение очередной итерации алгоритма Форда — Беллмана на всех узлах системы трудно в реализации и, более того, невозможно при наличии отказов отдельных узлов; 2) хотелось бы, чтобы алгоритм работал с произвольными начальными условиями, чтобы после конечного количества изменений в сети он продолжал строить наилучшие маршруты. Оказывается, что алгоритм продолжает корректно работать даже с произвольными начальными состояниями, а выполнять операции на различных узлах можно асинхронно и независимо от друг от друга.

Итого, распределенный асинхронный алгоритм Форда — Беллмана устроен следующим образом. Каждый узел \(i\) системы для каждого объекта назначения в момент времени \(t\) поддерживает оценку \(D_i(t)\) суммарной метрики \(D_i\) наилучшего маршрута до него (и соответствующий next hop). Узел регулярно рассылает своим соседям данные о своих текущих оценках. При получении оценки \(D_j^i(t)\) от своего соседа \(j\) узел \(i\) обновляет текущую оценку: \(D_i(t) := \min\big(D_i(t),\ \omega(i, j) + D_j^i(t)\big)\). Если при этом узел \(j\) являлся next hop, то происходит безусловное обновление текущей оценки: \(D_i(t) := \omega(i, j) + D_j^i(t)\). Таким образом, все необходимые для работы алгоритма данные находятся на соседних узлах, а в их памяти достаточно держать лишь таблицу маршрутизации. В этом заключается дистанционно-векторный подход к динамической маршрутизации: последовательность из начального узла и следующих next hop представляет из себя маршрут в виде вектора, суммарная метрика которого оценивается на начальном узле без поддержания базы данных состояния каналов.

Чтобы не перегружать статью математическими выкладками, сформулируем лишь идею доказательства корректности описанного алгоритма. Доказательство проходит в предположении, что любой узел никогда не перестает получать обновления от соседей. Поэтому важной частью системы также является механизм рассылки данных обновлений, но о нем поговорим позже. Основная идея доказательства заключается в построении двух последовательностей \(\{ \underline{D}_i^{(k)} \}_{k = 0}^{\infty}\) и \(\{ \overline{D}_i^{(k)} \}_{k = 0}^{\infty}\) для каждого узла \(i\), таких что

\[\underline{D}_i^{(k)} \leq \underline{D}_i^{(k + 1)} \leq D_i \leq \overline{D}_i^{(k + 1)} \leq \overline{D}_i^{(k)}.\]

Эти последовательности получаются из моделирования стандартного алгоритма Форда — Беллмана с различными начальными условиями, причем обе они стабилизируются к \(\{ D_i \}_{i = 1}^n\). После этого показывается, что оценки \(D_i(t)\) на узлах находятся между элементами данных последовательностей:

\[\underline{D}_i^{(k)} \leq D_i(t) \leq \overline{D}_i^{(k)}.\]

Таким образом, реальные оценки на узлах будут «зажиматься» между \(\underline{D}_i^{(k)}\) и \(\overline{D}_i^{(k)}\), и в конечном счете будут равны суммарным метрикам наилучших маршрутов. Подробное доказательство можно посмотреть в книге D. Bertsekas и R. Gallager «Data Networks» [3].

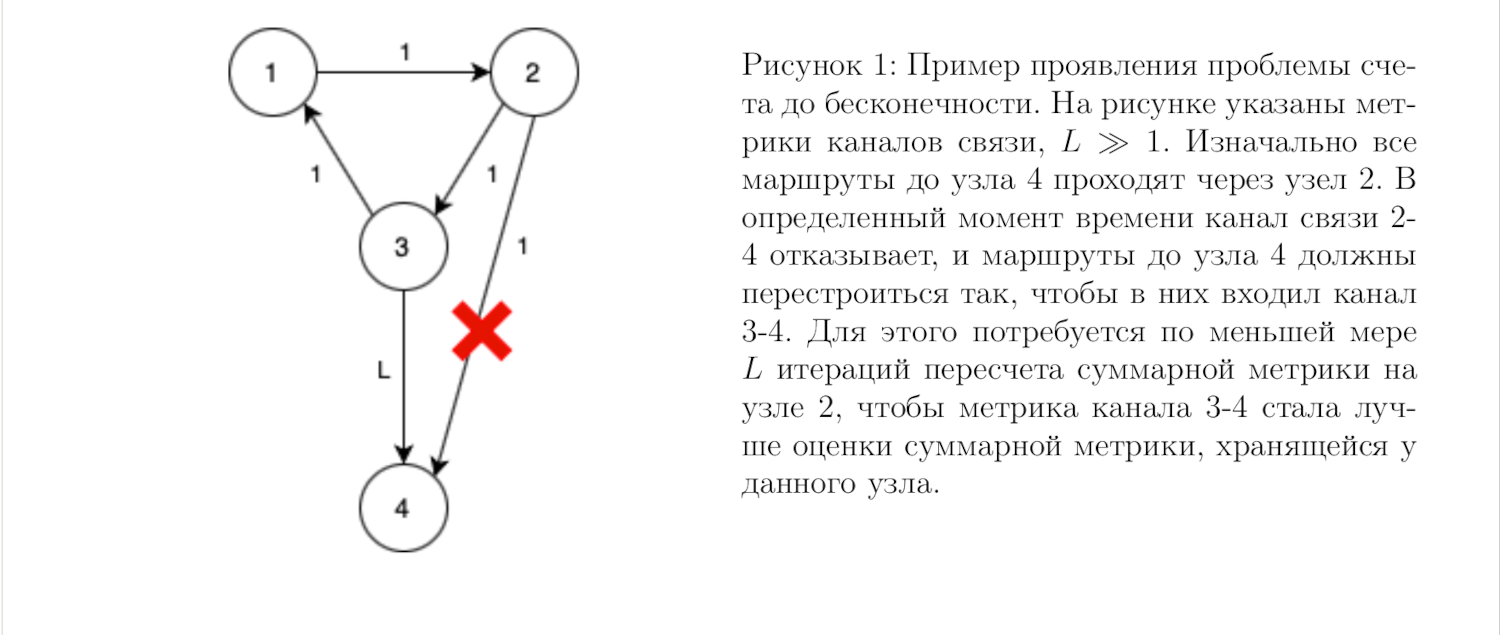
Существует и другое, в некоторой степени более конструктивное доказательство, в котором по индукции показывается, что со временем будут правильно построены все маршруты, начиная от имеющих наименьшую суммарную метрику и заканчивая самыми длинными. Однако в обоих доказательствах есть схожая особенность: каждое из них использует индукцию по множеству возможных значений суммарной метрики. Это, в свою очередь, может быть связано с известным недостатком подхода Distance Vector, проблемой счета до бесконечности (рис. 1).

4   Рассылка оценок соседям

Мы уже говорили о том, что в распределенном варианте алгоритма Форда — Беллмана важной составляющей является процесс рассылки текущего состояния таблицы маршрутизации соседям. Это можно организовать несколькими способами, которые мы кратко обсудим.

Первый способ имеет название «флудинг». Узел, инициирующий рассылку старается отправить данные всем своим соседям. Каждый узел при получении сообщения, отправленного в процессе флудинга, делает то же самое, и так далее. В конце концов информация  «расползается» по всей сети, причем если между начальным узлом и некоторым узлом назначения существовал рабочий путь, вероятнее всего в процессе флудинга данные до него дойдут. Однако этот способ обладает и некоторыми недостатками: очевидно, рассылка будет проходить неоптимальным образом, более того, если нам необходимо отправить данные лишь смежным узлам, способ оказывается избыточным, ведь флудинг затрагивает и более отдаленные узлы. Поэтому его обычно используют именно в тех случаях, когда нужно передать данные небольшого объема на все узлы системы. Например, флудинг используется в том же OSPF при рассылке обновлений о состояниях каналов в пределах зоны.

Другой способ основан на оптимизации, которую дают промежуточные результаты работы алгоритма динамической маршрутизации, и заключается в рассылке данных по остовному дереву. Изначально для этого нужно сформировать сообщение, содержащее информацию о множестве узлов назначения. При обработке сообщения такого типа заводится словарь, в котором ключи — это текущие next hop до узлов, содержащихся в списках-значениях. После этого данные передаются каждому из next hop также с указанием узлов назначения. В итоге рассылка происходит по остовному дереву, которое при правильной работе алгоритма динамической маршрутизации в конце концов станет минимальным остовом.

5   Приемы для борьбы с нестабильностью оборудования

В заключение поговорим о том, как описанные конструкции работают в реальной жизни, а именно обсудим несколько полезных приемов, применимых в проектировании распределенных систем и в протоколе обмена данными для реализации алгоритма динамической маршрутизации в частности.

5.1   Sequence numbers

Каждый из способов реализации операции рассылки, которые мы обсудили в прошлом разделе, подвержен проблемам реордерингов и повторов сообщений. Для наглядности опишем примеры, когда в каждом из способов сообщения могут приходить на отдельные узлы в порядке, отличном от того, в котором они были отправлены.

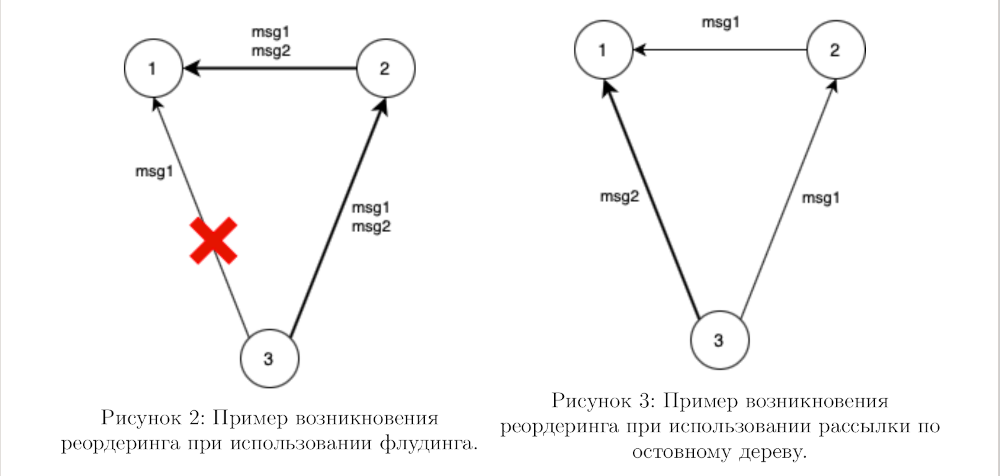
Пусть в системе, изображенной на рисунке 2 рассылка данных происходит с помощью механизма флудинга, причем передача данных по маршруту 3-2-1 проходит существенно быстрее, чем по каналу 3-1. Представим, что узел 3 генерирует два последовательных сообщения msg1 и msg2 для своих соседей и отправляет их узлам 1 и 2, но после отправки первого сообщения происходит отказ канала 3-1, и сообщение msg2 по нему не доставляется. Узел 2 при получении сообщений msg1 и msg2 в соответствии с логикой флудинга отправит их узлу 1 по каналу 2-1. В конце концов сообщения, проходящие по маршруту 3-2-1, дойдут до узла 1 раньше, чем сообщение msg1, отправленное по каналу 3-1. Если алгоритм чувствителен к порядку обработки сообщений, без дополнительной логики сообщение msg1 будет обработано последним, что может привести к некорректной работе.

Аналогичная проблема может возникнуть и при использовании рассылки данных по остовному дереву — пример изображен на рисунке 3. После отправки первого сообщения msg1 маршрут мог перестроиться, так что второе сообщение msg2 было отправлено по более быстрому пути. Таким образом, и в этом случае реордеринг сообщений может произойти.

Для того, чтобы бороться с реордерингами, а также повторными сообщениями, которые неизбежно будут возникать при флудинге, можно использовать прием под названием «sequence numbers». Он подразумевает добавление к сообщениям монотонно возрастающего со временем значения (версии) для того, чтобы отличать актуальные обновления от устаревших. Каждый узел при этом хранит словарь, в котором ключами являются идентификаторы узлов системы, а значениями — порядковое значение последнего полученного от соответствующего узла сообщения. Иногда к ключам данного словаря и самим сообщениям добавляются различные тэги, говорящие о том, к какому потоку сообщений они относятся — это позволяет переиспользовать механизм рассылки данных для произвольных целей, а не только для распространения информации о маршрутизации. При получении очередного сообщения его версия сравнивается с соответствующим значением в словаре, и если она строго больше его, полученное сообщение обрабатывается нужным образом, а версия в словаре обновляется, иначе только что полученное сообщение игнорируется.

Версии сообщений могут быть инкрементальными. Тогда помимо решения проблемы реордерингов узел-получатель сможет выявлять пробелы в потоке сообщений и сигнализировать об этом отправителю. В таком виде данный прием активно используется в протоколе транспортного уровня TCP [4, с. 24]. Если же у нас нет необходимости отслеживать доставку каждого сообщения, версии можно изменять таким образом, что механизм будет продолжать корректно работать даже после перезапуска отказавшего узла. Поскольку единственное требование на sequnce numbers — это их монотонность, к сообщению в качестве версии можно добавлять интервал времени, прошедший с начала эпохи. Тогда монотонность получится сохранить даже между запусками одного и того же узла.

5.2   TTL

Другая проблема, с которой можно столкнуться при создании собственного протокола обмена сообщениями, состоит в возможном образовании циклов. Они могут возникнуть даже в правильно спроектированной системе: например, при частых изменениях топологии маршруты могут перестраиваться таким образом, что некоторое сообщение будет проходить по одним и тем же узлам неограниченное количество раз. Такие сообщения засоряют собой трафик сети и без дополнительных механизмов на длинной дистанции могут стать причиной ее перегрузок.

Для борьбы с бесконечно  «гуляющими» сообщениями к ним добавляют специальное целочисленное поле TTL, означающее максимально допустимое количество хопов (пересылок) перед моментом, когда сообщение будет проигнорировано и перестанет пересылаться далее. При инициации отправки поле TTL устанавливает равным некоторому натуральному числу, и перед каждой передачей по сети его значение уменьшается на единицу. Если узел получил сообщение с TTL равным \(0\), дальше оно не передается. Тем не менее, иногда данный прием используется немного не по назначению: при рассылке broadcast пакета можно явно выставить значение поля TTL равным \(1\), чтобы пакет был отправлен лишь непосредственным соседям узла.

5.3   Экстренные обновления

Последний прием, который мы обсудим, связан с оптимизацией протоколов динамической маршрутизации, который в некоторых случаях может снизить время схождения сети. Как правило жизненный цикл узла, участвующего в маршрутизации, включает в себя регулярную рассылку некоторой информации о состояниях каналов или о суммарных метриках маршрутов. Пока в сети не происходит отказов, все работает в штатном режиме. Однако в момент возникновения неполадки один или несколько маршрутов могут стать недоступными для передачи по ним данных, и основная задача протокола динамической маршрутизации как раз состоит в том, чтобы как можно быстрее эти маршруты перестроить. Скорее всего узлы, непосредственно взаимодействующие с объектом отказа, заметят проблему почти сразу, однако таймер рассылки данных мог сработать незадолго до возникновения неполадки, из-за чего другие узлы до следующей рассылки будут думать, что с испорченными маршрутами все в порядке. Вкупе с проблемой счета до бесконечности в дистанционно-векторном подходе это может вылиться в продолжительное разделение всей сети.

Описанная проблема может быть отчасти решена введением экстренных обновлений, которые обрабатываются по тому же алгоритму, что и регулярные сообщения, но генерируются при существенном ухудшении маршрутов. При использовании данного приема важно сделать так, чтобы об изменениях топологии узнали все узлы системы, для которых это могло быть важно, а не только лишь находящиеся рядом с инцидентом. Например, при использовании подхода Distance Vector можно ввести значение разности \(\Delta_{crit}\) суммарной метрики, превышение которого при обработке очередного сообщения будет генерировать экстренное обновление. Логика следующая: если \(D_i(t_{new}) - D_i(t_{old}) \geq \Delta_{crit}\), где \(D_i(t_{new})\) — новая оценка суммарной метрики, а \(D_i(t_{old})\) — старая, то генерируется соответствующее экстренное обновление. Тогда информация о неполадке «расползется» по всем маршрутам, проходящим через объект неполадки, не затронув те части системы, для которых это было неважно.

Заключение

На этом мы завершаем рассказ об адаптации алгоритмов поиска кратчайших путей в графах для задач динамической маршрутизации. Мы сформулировали инженерную задачу в близком к формальному виде, рассмотрели два основных подхода к ее решению: Link State и Distance Vector, распределенный асинхронный алгоритм Форда — Беллмана и описали полезные приемы для проектирования подобных распределенных систем в условиях, приближенных к реальным.

Список литературы

[1] Markus Schulze. A new monotonic, clone-independent, reversal symmetric, andcondorcet-consistent single-winner election method. Social Choice and Welfare, 36(2):267–303, July 2010.

[2] John Moy. Ospf version 2. STD 54, RFC Editor, Апрель 1998. http://www.rfc-editor.org/rfc/rfc2328.txt

[3] Dimitri Bertsekas and Robert Gallager. Distributed Asynchronous Bellman-FordAlgorithm, pages 404–410. Prentice-Hall, Inc., Englewood Cliffs, New Jersey07632, 1992.

[4] Jon Postel. Transmission control protocol, STD 7, RFC Editor, September 1981, https://www.rfc-editor.org/rfc/rfc793.txt

---

1. Если попытаться формализовать понятия стоимости и качества, то легко увидеть, что, как это часто бывает в жизни, они находятся в прямой зависимости — то есть, вообще говоря, невозможно так просто снизить одно и увеличить второе. Например, можно было бы снизить суммарное количество передаваемых между всеми узлами данных (стоимость), если выбрать одну площадку, на которой будет происходить редукция, и которая затем будет рассылать результат редукции всем остальным. Однако, по сравнению с реализацией, когда каждая площадка обменивается данными напрямую с каждой, увеличивается задержка, и падает отказоустойчивость системы, то есть, уменьшается качество. Таким образом, на практике необходимо искать баланс между данными целями, однако конкретный выбор не имеет отношения к дальнейшему изложению.↩