Введение

В одной из наших предыдущих публикаций [1] мы рассказывали о способе измерения интенсивности потока событий при помощи счетчика на основе экспоненциального распада. Оказывается, идея такого счетчика имеет интересное обобщение.

План погружения у нас следующий. Для начала рассмотрим и проанализируем несколько примеров того, как вообще считают события и оценивают интенсивность потока. Дальнейший шаг — увидеть обобщение, а именно — некоторый класс счетчиков, который мы называем u-моделью. После мы исследуем, какими полезными свойствами обладают u-модели, и предлагаем методику построения адекватной оценки интенсивности.

1   Какие бывают счетчики

Без ограничения общности можно считать, что счетчик событий описывается своим состоянием \(s\), которое по приходе события в момент времени \(t\) обновляется по некоторому правилу:
$$
s\mathop{\mapsto}^t s'.
$$
Состояние не обязательно выражается числом, но из соображений практической реализуемости можно считать, что оно представляется конечным набором битов.

В некоторых случаях события являются взвешенными, и при обновлении состояния требуется учитывать вес события \(w\):
$$
s\mathop{\mapsto}^{t,w} s'.
$$
Но для начала будем рассматривать простые невзвешенные события, а учет веса добавим потом, когда понадобится. Это будет совсем не сложно.

В этой статье мы ограничимся рассмотрением только детерминированных счетчиков, то есть таких, для которых правило обновления задается функцией \(s'=update(s,t)\). Но вообще в этот механизм бывает полезно добавить немного рандома, об этом мы недавно рассказывали [7] и, вероятно, продолжим еще.

Также должна быть возможность, зная состояние счетчика, оценить интенсивность потока. Вообще говоря, понятие интенсивности потока нетривиально, и позже мы его обсудим подробнее. Пока же будем просто считать, что к модели счетчика прилагается некоторая номинальная оценка в виде функции \(r(s,t)\), выписанная из каких-то конструктивных соображений.

1.1   Линейные счетчики: подсчет всех событий

Самое простое, что можно придумать, — простой подсчет количества событий, произошедших с момента запуска. То есть по приходе события делаем вот так:
$$
s \mapsto s + 1.
$$
Будем называть такие счетчики линейными.

Оценка представляет собой среднюю интенсивность за всю историю:
$$
r(s,t) = s/t.
$$

Некоторую проблему может составлять то, что счетчик может переполниться. Также есть вопросы к тому, как задать оценку — очень старые события оказывают такое же влияние на оценку, как и недавние.

1.1.1   Подсчет событий в скользящем окне

Для устранения вышеописанных недостатков линейных счетчиков можно подсчитывать количество событий не с сотворения мира, а только тех, что произошли не более чем \(T\) тактов назад. Этот временной интервал длины \(T\) обычно называется окном, причем скользящим, поскольку с каждым тактом смещается вперед.

Наивная реализация предполагает запоминать все события в окне, что требует \(O(T)\) памяти. Однако есть способы сэкономить ресурсы в обмен на снижение точности, как это делают, например, здесь [6]. Правило обновления выражается довольно сложно, а в роли оценки будет средняя интенсивность за время \(T\):
$$
r(s,t) = s/T.
$$

К сожалению, и эта разновидность линейных счетчиков для наших целей не подходит: снижение точности еще можно потерпеть, а \(O(\log T)\) по памяти и по сложности выходит слишком накладно даже при небольших \(T\).

1.2   EDecay: экспоненциальный распад

Идея распадных счетчиков навеяна известной концепцией радиоактивного распада [4]. Ее суть состоит в том, что с течением времени количество нераспавшегося вещества уменьшается со временем по экспоненциальному закону:
$$v(t) = v_0 e^{-\lambda t},$$
где \(v_0\) — количество вещества в начальный (нулевой) момент времени, \(\lambda\) — некоторый параметр, так называемая постоянная распада.

Удобней переписать это выражение в таком виде:
$$v(t) = v_0 \alpha^{-t},$$
заменив параметр. Более подробно о параметризации моделей счетчиков см. раздел A приложения.

На основе этого механизма можно построить счетчик событий, как было описано в нашей статье [1].

Будем по определению считать, что каждому типу события соответствует величина \(v\), имеющая физический смысл «количества вещества» и зависящая от времени, которая при наступлении события скачком увеличивается на единицу, а в остальное время уменьшается по приведенному выше экспоненциальному закону.

То есть, чтобы учесть новое событие, пришедшее в момент времени \(t\), сначала нужно применить распад, а затем увеличить счетчик на единицу:

\begin{equation*}
v_{new}(t) = v(t) + 1 \equiv v(t_0)\alpha^{-(t - t_0)} + 1,
\end{equation*}
где \(t_0\) — время прихода предыдущего события.

Чтобы этим можно было пользоваться, нужно придумать, как хранить счетчик в памяти. Самый простой способ представления состояния счетчика — пара чисел \((v, t_0)\), где \(t_0\) — время последнего обновления, а \(v\) — количество вещества в этот момент. В этом случае правило обновления и оценку можно записать так:

\begin{align*}
(v, t_0) &\mathop{\mapsto}^t (v \alpha^{-(t - t_0)} + 1, t) \\
r((v, t_0), t) &= v \alpha^{-(t - t_0)}.
\end{align*}

В статье [1] мы детально разбираем такие счетчики. Важной идеей, которую здесь уместно упомянуть, является более экономичное предстваление состояние счетчика в виде одного числа \(s\), так называемого абсолютного значения, несущего в себе всю необходимую информацию для работы со счетчиком.

Величина \(v\) не хранится явно в памяти, но может быть вычислена в любой момент. Хранится же значение \(s\), такое что в момент времени \(t\) величина \(v\) выражается следующим образом:
$$
v = \alpha^{s-t}.
$$

Не вдаваясь в подробности, скажем лишь, что при таком подходе правило обновления и оценка принимают вид:

\begin{align}
s &\mathop{\mapsto}^t t+\log_\alpha(1 + \alpha^{s - t}) \tag{1}\\
r(s, t) &= \alpha^{s - t}.\nonumber
\end{align}

1.3   QDecay: более быстрый распад

При рассмотрении модели экспоненциального распада можно заметить, что функция распада (в данном случае экспонента) удовлетворяет дифференциальному уравнению:
$$\frac{dv}{dt} = -\lambda v.$$
На самом деле, с физической точки зрения, скорее, наоборот — именно это уравнение описывает радиоактивный распад, а экспонента — его решение.

Действительно, смысл уравнения состоит в том, что скорость распада пропорциональна количеству имеющегося вещества. В какой-то момент нам захотелось, чтобы распад в модели происходил побыстрее, для этого мы попробовали взять не линейную, а квадратичную зависимость (quadratic decay, QDecay):
$$\frac{dv}{dt} = -\lambda v^2.$$
Решение — новая функция распада:
$$
v(t) = \frac{1}{\lambda t + 1/v_0},
$$
и она действительно стала покруче.

На самом деле вряд ли корректно говорить, что гипербола круче экспоненты. Но распад больших значений теперь и правда происходит быстрее (а малых — медленнее).

Аналогично рассмотренной ранее модели (с экспоненциальным распадом), здесь можно представить состояние счетчика в виде одного числа \(s\). Соответствующее правило обновления и оценка интенсивности выглядят так:

\begin{align}
s &\mathop{\mapsto}^t t - \frac{t-s}{1 + \lambda(t - s)} \tag{2}
\\
r(s, t) &= \frac{1}{\lambda(t - s)}.\nonumber
\end{align}

Здесь замечательно то, что вычисление функции обновления обходится дешево — оно требует только элементарных арифметических операций, причем деление только одно. То есть изначально мы хотели всего лишь более быструю лошадь (распад), а получили новое полезное качество (меньше вычислений).

Можно пойти дальше, взяв бо́льшую степень в уравнении на функцию распада: \(dv = -\lambda v^3 dt,\) и так далее, но решение получается сложнее, вычисления дороже, а явной выгоды как-то не заметно. Не пригодилось.

1.4   SW: усреднение межпакетных интервалов

Рассмотрим еще один подход к построению счетчиков, а именно — усреднение. В данном случае будем усреднять интервал времени между соседними событиями. Мы называем эту величину межпакетным интервалом, поскольку имеем дело с сетевым трафиком, где в качестве события выступает приход сетевого пакета, а слово «межсобытийный» как-то не прижилось.

Вообще говоря, смысл этого подхода заключается в том, что у нас есть последовательность значений некоторой величины (в данном случае межпакетных интевалов), которая слишком быстро меняется, чтобы ее можно было использовать непосредственно, и хочется эту последовательность каким-то образом сгладить или усреднить.

Определение (усреднение). Пусть есть некоторая последовательность \(\langle p_n\rangle\), тогда ее среднее на \(n\)-м шаге определяется так:
$$
\overline{p}_n = \frac{1}{n} \sum_{i = 1}^n p_i.
$$
То есть здесь получается среднее арифметическое последних \(n\) членов последовательности.

Это определение можно обобщить. Взвешенным средним последовательности \(\langle p_n\rangle\) называется сумма
$$
\sum_{i = 1}^n \omega_i p_i,
$$
где \(\omega_i\) — некоторые весовые коэффициенты, такие что \(\omega_i\ge 0, \sum_{i}\omega_i=1\).

Напомним, что чем новее события, тем интереснее нам их вклад в оценку интенсивности. Поэтому вместо обычного усреднения естественно использовать взвешенное, давая больший вес недавним событиям. Выбирать веса можно по-разному, сейчас попробуем взять веса в виде членов геометрической прогрессии. Такой способ суммирования называется экспоненциальным скользящим средним (EMA).

Определение (EMA-усреднения). Экспоненциальное скользящее среднее последовательности \(\langle p_n\rangle\) определяется следующим образом:
$$
\overline{p}^{EMA}_n = \frac{1}{B}\sum_{i = 1}^n (1-\beta)^{n-i} p_i,
$$
где \(\beta\in(0,1)\) — параметр, \(B=\sum_{i = 1}^n (1-\beta)^{n-i}\).

Поскольку событий очень много, то есть \(n\) велико, можно считать, что в далеком прошлом были какие-то фиктивные события \(p_i\), \(i<0\), вклад которых берется с пренебрежимо малыми весами \(q^{n-i}\). Тогда удобней переписать определение так:
$$
\overline{p}^{EMA}_n = \beta\sum_{i = -\infty}^n (1-\beta)^{n-i} p_i,
$$
поскольку в этом случае \(B=\sum_{i = -\infty}^n (1-\beta)^{n-i} = 1/\beta\).

Одним из важных преимуществ EMA по сравнению с другими способами усреднения является возможность свернуть громоздкую сумму в рекурсивное выражение:

\begin{equation}\tag{3}
\overline{p}^{EMA}_n = \beta\cdot p_n + (1-\beta)\cdot \overline{p}^{EMA}_{n-1}.
\end{equation}
Таким образом, при вычислениях не требуется хранить множество старых значений \(p_n\). Кстати, именно формулу (3) часто берут в качестве опредения EMA [2].

Применяя формулу экспоненциального усреднения к межпакетным интервалам, получим:
$$
v_n = \beta\cdot (t_n-t_{n-1}) + (1-\beta)\cdot v_{n-1},
$$
где \(v_n\) — искомый EMA-усредненный межпакетный интервал, \(t_n\) — момент наступления \(n\)-го события.

Эта модель еще раз упоминается в разделе 4.3, где, в частности, показано, как выразить состояние счетчика одним числом и упростить вычисления. Пока же просто выпишем результат.

Обновление счетчика по приходе события в момент времени \(t\):

\begin{equation}\tag{4}
s \mathop{\mapsto}^t t + \beta\cdot(s-t).
\end{equation}

В качестве оценки интенсивности берется обратная величина усредненного значения межпакетного интервала:
$$
r(s,t) = -\frac{\beta}{1-\beta}\cdot\frac{1}{s-t}.
$$

Замечание. При помощи EMA-усреднения можно получить модель, в точности совпадающую с распадной моделью из раздела 1.2. Для этого надо усреднять не межпакетные интервалы, а величину \(p_t\), которую можно было бы назвать мгновенной интенсивностью:
$$p_t = \left\{\begin{array}{ll}1, & \mbox{если в момент t произошло событие},\\0, & \mbox{иначе}.\end{array}\right.$$

1.5   Вероятностные счетчики

Идея вероятностных счетчиков — менять состояние счетчика по приходе события не всегда, а с некоторой вероятностью. Эту вероятность можно задавать по-разному, например

• держать ее постоянной (биномиальные счетчики);
• уменьшать в 2 раза после каждого успешного обновления (счетчики Морриса);
• менять после каждых \(X > 1\) успешных обновлений.

Вероятностные счетчики позволяют очень эффективно использовать память. Например, оригинальные 8-битные счетчики Морриса можно использовать для учета до \(2^{256}\) событий. Очевидным же их недостатком является значительная ошибка при оценке числа событий. Мы подробно разбираем такие счетчики в статье [7], а также предлагаем некоторые расширения известных алгоритмов.

2   U-модель: идея

Если посмотреть на счетчики, основанные на идее распада, то можно заметить такую особенность: состояние описывается парой чисел \((v, t)\), но потом чудесным образом удается выразить состояние одним числом \(s\). Попробуем найти общий принцип, по которому это становится возможно для любых счетчиков такого типа.

Временно забудем тот факт, что на практике значение счетчика должно быть дискретно и описываться сравнительно небольшим количеством бит, и, оставаясь в рамках вакуумной сфероиппологии, положим, что и значение счетчика, и время прихода событий являются вещественными числами, а также преобразования над ними будут, соответственно, вещественнозначными. Потом (см. раздел 3.3) научимся дискретизировать модели, делая их пригодными на практике.

2.1   Инвариант распада

Рассмотрим участок кривой распада (см. рис. 1a). Пусть в момент времени \(t_0\) было зарегистрировано событие, и потом на интервале \([t_0, t)\) других событий не было. Сейчас находимся в точке \(t\) и собираемся учесть новое событие или хотя бы просто посмотреть, какова величина \(v\) в этот момент, чтобы оценить интенсивность. Можно заметить, что с точки зрения наблюдателя, находящегося в моменте \(t\), нет совершенно никакой разницы, находится ли последнее событие на графике в точке \((t_0, v_0)\) или же в точке \((t'_0, v'_0)\). Сей факт как бы намекает, что хранить два числа в качестве состояния — явно избыточно. Таким образом, два формально разных варианта реальности функционально эквиалентны, то есть дают один и тот же эффект:
$$
(t_0,v_0) \sim (t'_0, v'_0).
$$

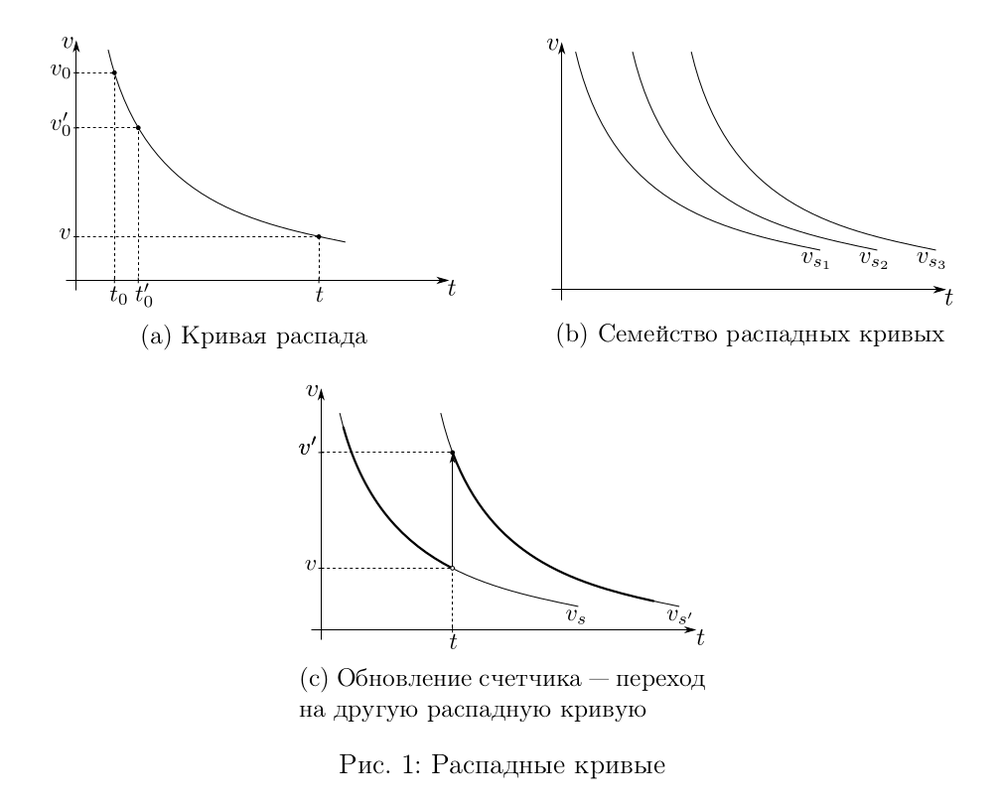
Вообще говоря, у нас не одна распадная кривая, а целое семейство \(v=v_s(t)\) (см. рис. 1b). Каждая из этих кривых описывает одно и то же состояние. Их можно некоторым образом занумеровать, и в качестве состояния счетчика взять номер, точнее, индекс кривой.

Посмотрим теперь, как должно происходит обновление такого счетчика. Пусть \(s\) — текущее состояние счетчика. Согласно распадной модели, это значит, что при отсутствии событий значение \(v\) с течением времени будет меняться, оставаясь на кривой \(v_s(t)\). Пусть в некоторый момент времени \(t\) происходит событие. Это значит, что величина \(v\) скачком увеличивается на единицу (см. рис. 1c), то есть среди всего семейства кривых надо найти ту, которая проходит через точку \((t, v')\), где \(v'=v+1\). Пусть \(s'\) — индекс этой кривой, то есть

\begin{equation}\tag{5}
v_{s'}(t) = v_s(t) + 1,
\end{equation}

тогда именно это значение \(s'\) нужно записать в качестве нового состояния счетчика.

Замечание. Если нужно учитывать взвешенные события, то изменение происходит не на единицу, а на вес события: \(v'=v+w\).

Пока не очень понятно, как находить индекс нужной кривой, но совсем скоро это прояснится.

2.2   Трансляционная симметрия

На рис. 1b распадные кривые \(v_s(t)\) изображены так, что они отличаются друг от друга только сдвигом по горизонтали. По-научному это называется трансляционная симметрия времени [8]. Мы хотим взять это свойство в качестве аксиомы для нашей модели счетчика. Действительно, логично ожидать, что в рамках модели распад сегодня происходит в точности так же, как вчера.

Математически это можно свойство записать так:
$$
\forall t\in\mathbb{R}\colon v_{s_2}(t) = v_{s_1}(t-\Delta),
$$
то есть кривая \(v_{s_2}(t)\) получается из кривой \(v_{s_1}(t)\) сдвигом вправо на некоторую величину \(\Delta\).

Вообще кривые можно занумеровать как попало, нужно лишь уметь находить индекс новой кривой при операции обновления. Но удобнее всё же нумеровать по порядку, так чтобы индекс \(s\) представлял собой что-то осмысленное, а именно — вещественное число, соотвествующее расстоянию по горизонтали между данной кривой \(v_s(t)\) и кривой с нулевым индексом \(v_0(t)\). Тогда, благодаря трансляционной симметрии, любая кривая из семейства очень просто выражается через кривую номер ноль:

\begin{equation}
\forall t,s\in\mathbb{R}\colon v_s(t) = v_0(t-s)\equiv \mu(s-t).\tag{6}
\end{equation}

Замечание. Здесь введено обозначение \(\mu(x) := v_0(-x)\), которое удобно тем, что функция \(\mu\) монотонно возрастает. Это потом пригодится в разделе 2.4 при определении интенсивности.

Теперь правило обновления по приходе события в момент времени \(t\) можно выразить из уравнения (5) следующим образом:
$$
s' = t + u(s-t),\quad \text{где }
$$

\begin{equation}
u(x) = \mu^{-1}(\mu(x) + 1).\tag{7}
\end{equation}

Таким образом, правило обновления представляется в виде

\begin{equation}\tag{8}
s \mathop{\mapsto}^t t + u(s-t),
\end{equation}
где \(u(\cdot)\) — некоторая функция.

Это правило выглядит настолько просто и универсально, что его можно взять в качестве определения. Именно так мы будем определять u-модель.

Замечание. Если распадная функция задается дифференциальным уравнением вида
$$
\frac{dv}{dt} = f(v),
$$
то для нее всегда легко находится инвариант, который обладает свойством (6).

Действительно, решение дифференциального уравнения можно записать в виде
$$
F(v) - F(v_0) = t - t_0,\quad\mbox{где } F(v) = \int \frac{dv}{f(v)}.
$$
Тогда в качестве инварианта можно взять \(s = t_0-F(v_0)\), а соответствующая кривая выражается как \(v_s(t)=F^{-1}(t-s)\).

В разделе 3.1 перечислены формальные свойства, которым должна удовлетворять функция \(u\), чтобы на ее основе построить работоспособную модель счетчика.

2.3   Абсолютное и относительное

Можно сказать, что \(s\) — это абсолютное значение счетчика, оно хранится непосредственно в памяти, а \(x=s-t\) — относительное значение счетчика в момент времени \(t\). Тогда получается, что функция обновления работает с относительным значением счетчика: \(x' = u(x)\).

Тот факт, что функция обновления работает с относительным значением счетчика, отражает принцип распада: если события не происходят, то абсолютное значение \(s\) не меняется, а относительное — автоматически убывает с течением времени. И оценка интенсивности, соответственно, тоже будет падать. С точки зрения вычислений очень удобно — пока событий нет, ничего делать не надо. Очень похоже на инфляцию в экономике: состояние счетчика — это банкноты, лежащие под подушкой, а оценка интенсивности — покупательная способность этих банкнот, которая сама собой деградирует.

2.4   Оценка интенсивности

Для распадной модели значение \(\mu(s-t)\) по построению является оценкой интенсивности (см. формулу (6)). Однако с таким определением возникают некоторые проблемы. Во-первых, если мы используем определение модели через функцию \(u\), построить функцию \(\mu\) будет затруднительно (пришлось бы решать функциональное уравнение (7)). Во-вторых, было бы неплохо проверить экспериментально, насколько адекватно конкретный счетчик измеряет интенсивность.

Сохраняя не букву (из формулы (6)), но дух идеи распда, будем строить оценку интенсивности как функцию от одного аргумента, а именно — от относительного значения счетчика: \(r(s, t) = r(s-t)\). Таким образом, задача ставится так: имея функцию обновления \(u(x)\), построить фукнцию \(r(x)\), которая была бы адекватной оценкой интенсивности.

Получается, что подход u-модели состоит в реализации следующего плана (да, выглядит несколько по-панковски).

1. Берем какие-нибудь модели, построенные из «физических соображений», и для каждой из них выражаем правило обновления через u-функцию.
2. Затем абстрагируемся от физического смысла, оставляя только голую u-функцию. Теперь можно, не заботясь о смысле, смело менять u-функцию, например, выбирая более вычислительно дешевую.
3. Наконец, придумываем, как заново внести смысл — построить адекватную оценку интенсивности.
4. PROFIT!

Для того, чтобы этот план стал возможным — загвоздка, очевидно, только в пункте 3, — потребуется наложить какие-то ограничения на u-функцию, и сейчас попробуем выяснить, какие именно. Эти мотивационные рассуждения, однако, можно пропустить и сразу перейти к определению ограничений (9) на u-функцию.

2.4.1   Равномерный поток

Наша компания занимаемся изучением трафика в сети, и мы можем считать приход сетевых пакетов штуками — это будет поток, интенсивность которого измеряется в пакетах в секунду (pps, packets per second). А можем учитывать размер пакетов, тогда размер выступает в качестве веса события, соответственно, интенсивность такого взвешенного потока будет измеряться в битах в секунду (bps, bits per second). Бывает также важным различать пакеты по их содержимому (IP-адреса источника и/или получателя, номера портов, протокол и т.п.), тогда мы группируем события по типам и для каждого типа заводим отдельные счетчики.

Поскольку мы здесь занимаемся оценкой интенсивности потока событий, нужно вначале формализовать понятия события и потока событий.

Определение (событие). Событием назовем тройку \((id, w, t)\), где \(t\) — время прихода события, \(w>0\) — вес события, \(id\) — тип события, некоторый идентификатор потока.

Определение (поток событий). Поток событий определяется как последовательность событий \(\mathcal{E}_k=(id_k,w_k,t_k)\),  \(k\in\mathbb{Z}\). Причем события в потоке должны быть упорядочены по времени: \(t_i\le t_j\) при \(i<j\).

В большинстве реализаций систем учета событий время считается дискретной величиной: \(t_k\in\mathbb{Z}\), однако для теоретических рассуждений бывает удобно обобщить и считать время непрерывным: \(t_k\in\mathbb{R}\).

Если нас интересуют только события как таковые, например, мы измеряем количество пакетов штуками в секунду, то вес \(w\) можно полагать равным единице. Предполагается также, что отдельный счетчик учитывает события одного типа, то есть поле \(id\) служит для различения разных потоков и не играет роли рамках одного счетика.

Определение (равномерный поток). Детерминированный равномерный поток \(\langle t_k\rangle\) определяется следующим образом:
$$
t_k = pk,\quad k\in\mathbb{Z},
$$
где \(p>0\) — параметр потока — период между событиями. Тогда интенсивность такого потока, по определению, выражается как \(r=1/p\).

Теперь можно выразить способ измерения интенсивности потока для любой модели. Пусть на счетчик набегает поток некоторой известной интенсивности \(r\), и мы наблюдаем, как меняется относительное значение счетчика — пусть после \(n\)-го события измеренное значение счетчика равно \(x_n\).

Хочется, чтобы интенсивность потока \(r\) и последовательность значений \(x_n\) были как-то связаны между собой. Тогда, если повезет, мы могли бы построить функцию оценки интенсивности \(r(x)\).

2.4.2   Аттрактор

Изучая на конкретных примерах поведение u-модели под воздействием детерминированного потока, мы обнаружили, что (по крайней мере для этих примеров) существует понятие аттрактора, который не вполне формально описывается следующими свойствами.

• Для каждого значения интенсивности входящего потока \(r\) существует аттрактор — такое подмножество относительных значений счетчика, что если какое-то значение \(x_N\) оказалось в этом аттракторе, то все последующие значения \(x_n\) для \(n\ge N\) туда тоже попадут. Аттрактор представляет собой отрезок \([\check{x}, \hat{x}]\) (возможно, вырожденный, когда оба его конца слиплись).
• Имеет место сходимость — даже если относительное значение счетчика было вне аттрактора, по прошествии нескольких обновлений оно туда попадет или хотя бы подойдет сколь угодно близко к аттрактору.
• Имеет место монотонность — положение аттрактора монотонно зависит от интенсивности набегающего потока. То есть оба конца отрезка \(\check{x}(r)\) и \(\hat{x}(r)\) являются монотонно возрастающими функциями.

Поскольку нам нужно по значению счетчика судить об интенсивности потока, требуется решить обратную задачу. Это возможно в силу монотонности и непрерывности — существуют функции \(\check{r}(x), \hat{r}(x)\), такие что при попадании \(x\) в аттрактор, можно гарантировать, что истинное значение интенсивности лежит в интервале \([\check{r}(x), \hat{r}(x)]\).

Разумеется, для того чтобы эти свойства были практически полезными, нужно, чтобы, во-первых, отрезок-аттрактор был коротким, иначе точность будет низкой, во-вторых, чтобы сходимость была быстрой, иначе придется долго ждать, прежде чем счетчик начнет показывать адекватное значение. В любом случае для конкретной u-модели можно записать решение в явном виде и оценить точность и скорость сходимости.

Теперь попробуем перейти от частного к общему. Зададимся вопросом: какие условия нужно наложить на u-функцию, чтобы у соответствующей u-модели появился аттрактор с указанными выше свойствами? Исчерпывающий ответ изложен в следующем разделе.

3   U-модель: реализация

3.1   Определение u-модели

Пусть функция \(u\colon\mathbb{R}\to\mathbb{R}\) удовлетворяет следующим условиям:
\begin{gather}
u(x)\text{ возрастает},\tag{9a}\\
\Delta u(x) \ge 0\text{ при всех }x,\tag{9b}\\
\Delta u(x)\text{ убывает},\tag{9c}\\
\Delta u(+\infty)=0,\tag{9d}
\end{gather}
где \(\Delta u(x) = u(x)-x\).

Определение (u-модель). Рассмотрим способ обновления счетчика, построенный на основе функции \(u\), обладающей свойствами (9), при котором обновление счетчика \(s\) по приходе события в момент времени \(t\in\mathbb{R}\) выражается правилом (8):
$$
s\mathop{\mapsto}^t t + u(s-t).
$$

Такой способ обновления счетчика назовем u-моделью обновления.

Функция \(u\), удовлетворяющая условиям (9), обладает некоторыми полезными свойствами. Например, функция \(u\) (а также \(\Delta u\)) непрерывна. Это доказывается из свойств (9a) и (9c) с помощью \(\varepsilon\)-\(\delta\)-формализма.

3.2   Измерение интенсивности

Свойств (9) оказывается достаточно, чтобы обеспечить существование аттрактора и построить верхнюю \(\hat{r}\) и нижнюю \(\check{r}\) оценки интенсивности. На этот счет есть несколько теорем, часть из которых представлена в этом разделе, а часть осталась за кадром.

3.2.1   Строгая u-модель

Можно заметить, что условия (9) не запрещают случай, когда приращение функции обновления обращается в ноль в некоторой точке, то есть когда \(\exists x_{zero}\colon \Delta u(x_{zero})=0\). В этом случае \(\Delta u\) будет обращаться в ноль и при всех \(x>x_{zero}\). Обозначим
\begin{gather*}
X = \{x\mid \Delta u(x)>0\}\\
x_{max}=\sup X,\quad x_{max}\in\mathbb{R}\cup\{+\infty\}.
\end{gather*}
Несложно доказать, что если взять \(x_0\in X\) и применить к нему серию обновлений, то значения, бо́льшие чем \(x_{max}\), будут недостижимы — относительные значения счетчика никогда не выйдут за пределы \(X\). То есть \(X=(-\infty, x_{max})\) можно назвать рабочим диапазоном u-модели. Вне этого диапазона u-функция устроена тривиально, и ее поведение нам не интересно. Эта оговорка нужна, чтобы ввести понятие строгой u-модели.

Определение (строгая u-модель). Если в дополнение к свойствам (9) функции \(u\) и \(\Delta u\) являются строго монотонными на \(X\), то соответствующую u-модель обновления назовем строгой.

Теорема (теорема о неподвижной точке). Для строгой u-модели при воздействии детерминированного равномерного потока интенсивности \(r\) последовательность значений \(x_n\) является константной, если выполнено дополнительное условие: функция \(u\) является сжимающим отображением, то есть \(\exists \kappa\in(0,1)\), такое что \(\forall a \forall b\colon |u(a) - u(b)| < \kappa|a-b|\).

Идея доказательства заключается в применении теоремы Банаха [5], которая гарантирует существование и единственность неподвижной точки у сжимающего отображения. Тогда все члены последовательности \(x_n\) будут равны значению этой неподвижной точки.

Получается, что у строгой u-модели аттрактор состоит из одной точки.

На самом деле не для всех u-моделей, которые мы используем, функция обновления является сжимающим отображением, например, у модели EDecay функция обновления «почти» сжимающа — для нее константа \(\kappa\) равна единице, то есть теорема Банаха не работает. Но с точки зрения практического применения это не является проблемой, поскольку есть другие полезные теоремы.

Например, имеет место следующее утверждение. Если в некоторый момент времени счетчик находился в таком состоянии, что его относительное значение было равно \(x_0\), и на него начал поступать детерминированный поток событий, то последовательность его относительных значений \(x_k\) стремится к некоторому значению \(x^*\), причем известна скорость сходимости. В частности, для модели EDecay сходимость выглядит так: \(|x_k-x^*|\le C\alpha^{-(t_k-t_0)}\), что с практической точки зрения позволяет оценить, насколько быстро и адекватно модель реагирует на изменение характера трафика.

3.2.2   Общий случай — нестрогая модель

Что касается дискретизованных моделей (см. раздел 3.3), то они теряют строгую монотонность, поэтому вместо теоремы о неподвижной точке помогает набор утверждений (не приводим их здесь), которые требуют более слабых условий и дают более слабые, хотя всё еще полезные для оценки интенсивности, результаты.  Для нестрогой модели вместо взаимно однозначного соответствия между интенсивностью потока и относительным значением счетчика имеет место интервальная оценка. То есть аттрактор представляет собой невырожденный отрезок.

Пользуясь предложенной методикой, для заданной u-модели остается лишь построить верхнюю \(\hat{r}\) и нижнюю \(\check{r}\) оценки интенсивности, а также оценить скорость сходимости к аттрактору.

3.3   Дискретизация

Для того, чтобы u-моделью можно было пользоваться на практике, ее необходимо дискретизировать. То есть сделать так, чтобы множество состояний счетчика стало конечным, причем, желательно, небольшим по размеру. Почему небольшим? Нам нужно держать в памяти миллиарды счетчиков, чем их больше, тем выше будет качество предоставляемого сервиса. В самом деле, зачем тратить 64 бита на счетчик, когда можно обойтись 16-ю?

Замечание. Можно пойти на хитрость, усложнив представление состояния, представив его в виде пары \(s=(s_{local}, s_{global})\), где \(s_{local}\) относится к конкретному счетчику, а \(s_{global}\) — общая часть состояния целой группы счетчиков. Мы дейстительно пользуемся этим приемом, в частности, для борьбы с переполнением счетчиков, но в данной работе его не рассматриваем.

Один из очевидных способов дискретизации — из континуума относительных значений счетчика выбрать конечное подмножество идущих подряд целых чисел и немного модифицировать u-функцию, так чтобы она стала целочисленной.

Для начала построим функцию \(u^\sqcup\colon \mathbb{R}\to\mathbb{R}\), такую что:

• она имеет целые значения в целых точках: \(u^\sqcup(n) \in \mathbb{Z}\) для \(n\in\mathbb{Z}\),
• в некотором смысле близка к \(u\): \(u^\sqcup(n)\approx u(n)\) для \(n\in\mathbb{Z}\),
• удовлетворяет условиям (9).

По-видимому, эту задачу можно решить разными способами. Ниже приведен один конкретный способ построения \(u^\sqcup\).

Основная идея этого построения состоит в том, чтобы задать значения \(u^\sqcup\) в целых точках путем округления вниз, то есть \(u^\sqcup(n):=\lfloor u(n)\rfloor\) для \(n\in\mathbb{Z}\), потом достроить \(u^\sqcup\) в промежуточных точках так, чтобы сохранить непрерывность и монотонность (условия (9)).

Удобней сначала строить \(\Delta u^\sqcup\), а потом через нее определить \(u^\sqcup\). Для этого зафиксируем \(\Delta u^\sqcup\) в целых точках, а в промежуточных сделаем линейную интерполяцию. Это можно записать так:
$$
\Delta u^\sqcup(x) = (1-\varepsilon)\Delta u(n) + \varepsilon\Delta u(n+1),
$$
где \(n=\lfloor x\rfloor,\) \(\varepsilon = \{x\}\) — соответственно, целая и дробная часть аргумента.

Остается лишь определить саму функцию \(u^\sqcup(x)\):
$$
u^\sqcup(x) = \Delta u^\sqcup(x) + x.
$$

Утверждение. Построенная таким образом функция \(u^\sqcup\) удовлетворяет условиям  (9) и, таким образом, определяет u-модель.

Замечание. Вообще говоря, u-модель при такой операции (переход от \(u\) к \(u^\sqcup\)) немного портится — если она была строгой, то после преобразования перестает быть таковой.

Возникает закономерный вопрос: зачем доопределять \(u^\sqcup\) в промежуточных (нецелых) точках, если мы планируем производить вычисления только над целыми значениями счетчика? Дело в том, что помимо правила обновления нам необходимо построить еще оценку интенсивности, а для этого проще всего воспользоваться методом чайника — достроить \(u^\sqcup\) в нецелых точках и получить новую u-модель (вылить воду из чайника), чтобы потом воспользоваться теоремами, связывающими наблюдаемое значение счетчика с оценками интенсивности (свести задачу к предыдущей).

Кажется, здесь должна быть какая-то метатеорема, утверждающая, что, независимо от способа построения \(u^\sqcup\) в промежуточных точках, методика построения оценок дает одинаковый результат.

Теперь у нас есть функция \(u^\sqcup\), которая порождает u-модель и в целых точках принимает целые значения. Осталось позаботиться о том, чтобы ограничить ее на конечном интервале, чтобы значения счетчика не расползались до бесконечности. Для этого возьмем целочисленный интервал \(X^\square=\{x_{min},\dots, x_{max}\}\) и ограничим \(u^\sqcup\) на нем, то есть получим функцию \(u^\square\colon X^\square\to X^\square\), которая совпадает с \(u^\sqcup\) на области определения.

Замечание. Как выбирать границы интервала. В качестве \(x_{max}\) следует взять такое число, чтобы \(\Delta u^\square(x_{max})=0\), \(\Delta u^\square(x_{max}-1)>0\). (В силу условия (9d) такое число существует.) Тогда результат обновления никогда не вылезет за правую границу: для \(\forall x\in X^\square\) имеем \(u^\square(x)\le x_{max}\). Что касается левой границы, то ее можно выбирать произвольно (годится любое \(x_{min} < x_{max}\)). Действительно, в силу неотрицательности \(\Delta u^\square\) для \(\forall x\in X^\square\) будет выполнено \(u^\square(x)\ge x \ge x_{min}\), то есть результат обновления не вылезет за левую границу. Таким образом, \(x_{min}\) можно выбирать из соображений размера счетчика — чем больше разрядность счетчика, тем левее можно подвинуть левую границу, и тем точнее будет оценка малоинтенсивных потоков.

Именно эту функцию \(u^\square\) (точнее, ее численную реализацию) будем использовать в алгоритме обновления счетчика.

В разделе B приложения в качестве примера показана дискретизация модели EDecay.

4   Примеры u-моделей

Как было показано выше, счетчики, введенные в разделе 1 (кроме линейных), представляются в виде u-модели. Здесь мы рассмотрим их еще раз, теперь уже в соответствии с новой методикой: вначале задается u-функция, потом строятся оценочные функции.

Рисунки 2,3,4 иллюстируют свойства моделей: оттенками желтого показаны графики функций \(u(x)\) и \(\Delta u(x)\), остальные графики — оценки интенсивности. Параметры моделей были подобраны таким образом, чтобы показать разницу между верхней и нижней оценкой. На практике мы используем такие значения параметров, чтобы оценки были поточнее. Если же, например, для модели EDecay взять \(\tau\) побольше (например, у нас в рабочем коде \(\tau\) составляет порядка \(10^8\)), то графики оценок визуально слипнутся, что, очевидно, свидетельствует о высокой точности модели.

4.1   EDecay

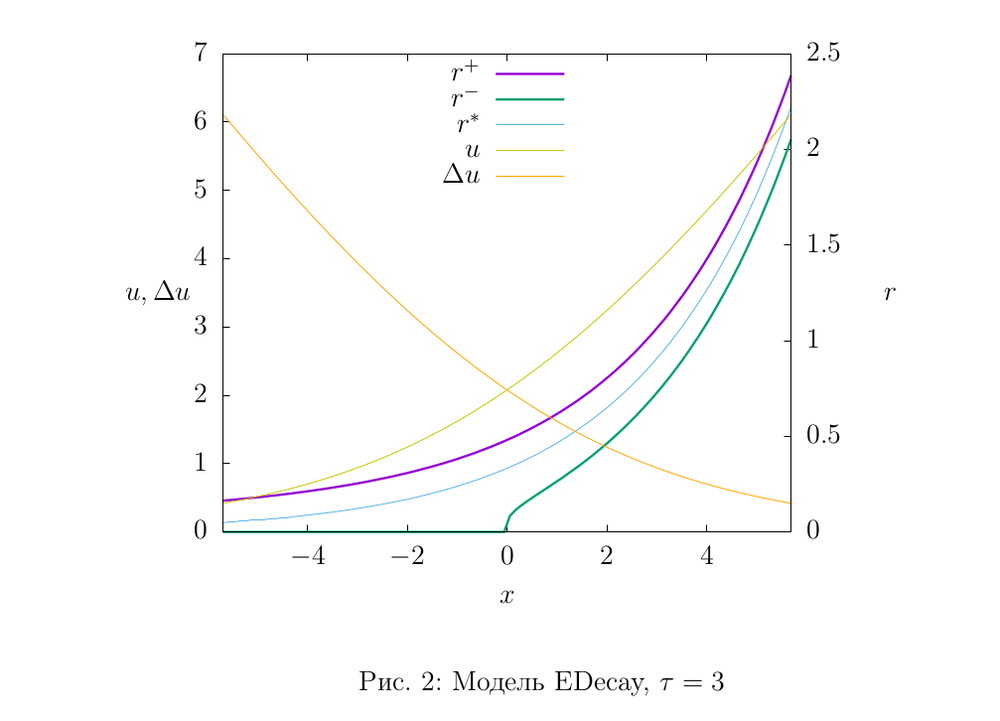
Правило обновления (1) выглядит так:
$$u(x) = \log_\alpha(1+\alpha^x),$$
где \(\alpha>0\) — параметр (см. раздел A приложения).

У этой модели есть интересная особенность — для нее существует оценочная функция \(r^*(x) = \alpha^x\) (ее график обозначен голубой линией на рис. 3), обладающая следующим свойством. Пусть имеется два счетчика, которые учитывают два разных потока событий, и третий счетчик, который учитывает сразу оба потока. Тогда для модели EDecay существует такая оценочная функция \(r^*(x)\), что в каждый момент времени \(t\) имеет место равенство:
$$r^*(s_1-t) + r^*(s_2-t) = r^*(s-t),$$
где \(s_1\) и \(s_2\) — абсолютное значение первых двух счетчиков, а \(s\) — абсолютное значение третьего. Логично назвать такое свойство модели аддитивностью. Оказывается, EDecay — единственная среди всех u-моделей, которая обладает этим свойством. Для остальных u-моделей это равенство может выполняться лишь приблизительно. Здесь, кстати, наглядно прослеживается аналогия с радиоактивным распадом — можно сказать, что эта оценка \(r^*(x)\) играет роль массы или количества вещества.

4.2   QDecay

Соответствующая правилу (2) функция обновления выглядит так:
$$u(x) = \frac{x}{1-x/\tau}.$$

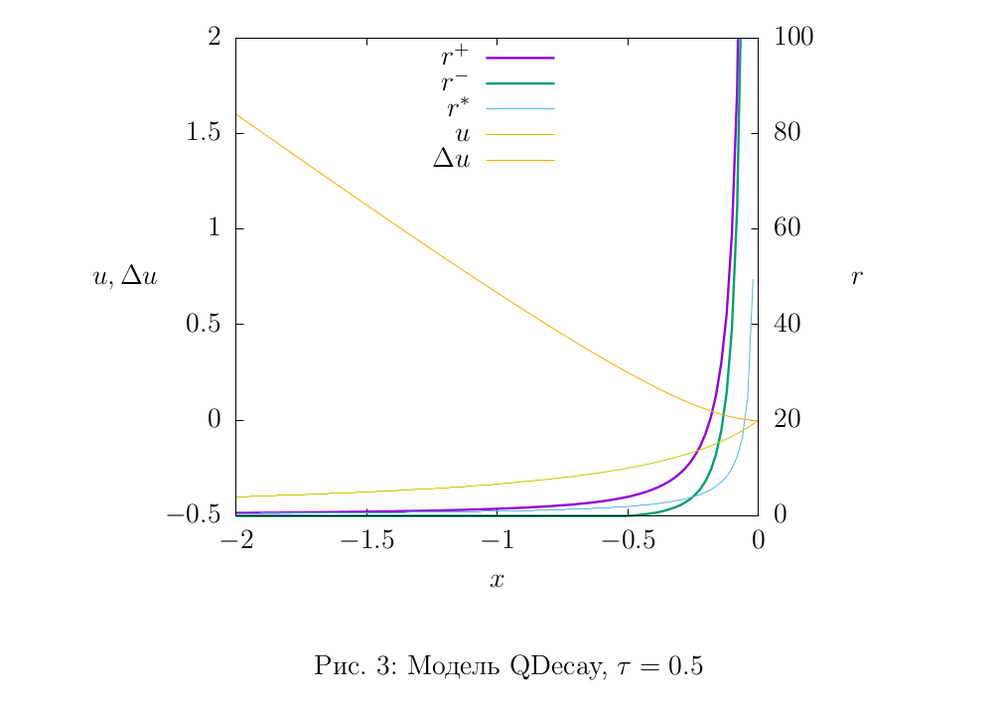
4.3   SW

Правило обновления (4) эквивалентно выражается в рамках u-модели через функцию обновления
$$u(x) = \beta x.$$
Полезным свойством этой модели является вычислительная простота функции обновления, можно прямо эту формулу записать в код безо всяких табличных приближений.

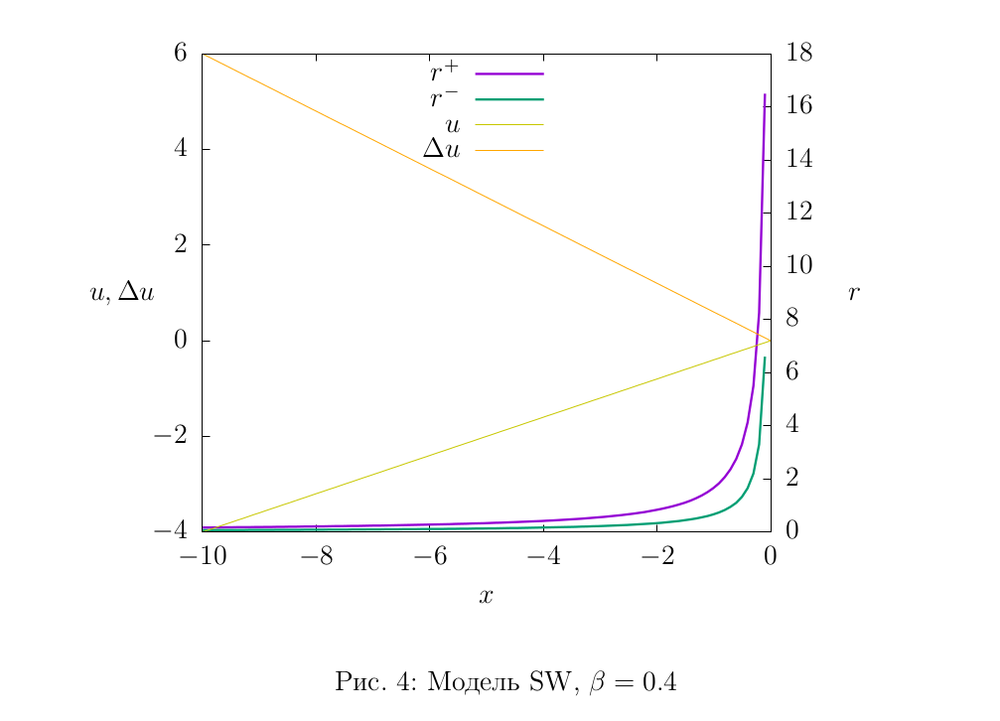
4.4   Сводная таблица

В таблице 1 указаны характеристики перечисленных моделей.

Можно заметить, что у некоторых моделей формула нижней оценки \(r^-\) при некоторых значениях аргумента становится бессмысленной. Это означает, что при таких (слишком малых) относительных значениях счетчика ничего нельзя сказать о том, насколько мала может быть интенсивность, поэтому мы полагаем нижнюю оценку просто равной нулю (меньше нуля-то интенсивность не бывает). Теоретически для некоторых u-моделей может случиться так, что и верхняя оценка \(r^+\) по какой-либо причине обессмысливается. В таких случаях следует полагать ее равной бесконечности.

Помимо строгих оценок интенсивности \(r^-\) и \(r^+\), выведенных в рамках общей методике u-моделей, указана также оценка \(r^*\), построенной «из физических соображений» (голубая линия на графиках). Ожидалось, что она всегда будет находиться между нижней и верхней оценками (\(r^-\) и \(r^+\)), однако в случае модели QDecay это не так — есть участок, где она меньше нижней оценки. Этот пример показывает полезность описываемого здесь подхода: каковы бы ни были соображения, по которым строится модель счетчика, всегда полезно лишний раз перепроверить, как воздействует поток известной интенсивности на состояние счетчика.

Заключение

На нескольких примерах были показаны общие принципы построения счетчиков событий. В качестве довольно универсального обобщения предложена схема u-модели. Предложена методика построения оценок интенсивности для любых u-моделей.

Кроме того, за кадром остались много интересного.

• Вероятностные счетчики. Что будет, если в правиле обновления u-модели заменить функцию \(u\) на случайную величину, зависящую от относительного значения счетчика?
• Представление и обслуживание больших массивов одинаковых счетчиков. Функции обновления и оценки завият от относительного значения счетчика \(x=s-t\), где \(s\) и \(x\) могут находиться в сравнительно узком диапазоне значений, в то время как \(t\) пробегает широкий (потенциально бесконечный) диапазон. Как сделать, чтобы счетчики не переполнялись?
• Алгоритмы выделения тяжелых потоков. Отдельные счетчики позволяют измерять интенсивность потоков, но как их организовать, чтобы выявлять наиболее интенсивные потоки?

Приложение

A   Параметризация

Все модели счетчиков, рассматриваемые в данной статье, являются однопараметрическими. Но мы в разных местах используем в качестве параметра разные величины, чтобы формулы выглядели удобней. Ниже следует перечень величин, каждая из которых может быть равноценно использована в качестве параметра модели, с указанием их физического смысла и взаимосвязей между ними.

• \(\lambda>0\) — так называемая постоянная распада из закона радиоактивного распада [4]$$v(t) = v_o e^{-\lambda t}.$$
• \(\tau>0\), \(\tau=1/\lambda\) — величина, характеризующая среднее время жизни в той же модели. Также верно, что за время \(\tau\) количество распадающегося вещества уменьшается в \(e\) раз, а период полураспда выражается через \(\tau\) следующим образом: \(T_{1/2}=\tau\ln2\).
• \(\alpha>1\), \(\alpha=e^\lambda\).
• \(\beta\in(0,1)\) — параметр сглаживания в EMA [2]
• $$v_n = \beta\cdot (t_n-t_{n-1}) + (1-\beta)\cdot v_{n-1}.$$ Модель экспоненциального распада может быть выражена двояко: через радиоактивный распад и через EMA-сглаживание. При этом имеет место связь между параметрами: \(\beta = 1-1/\alpha\).

B   Пример дискретизации EDecay

Модель EDecay определяется следующей функций обновления:
$$
u(x) = \log_\alpha(1 + \alpha^x).
$$
Рассмотрим на рис. 5, как меняется функция обновления при дискретизации.

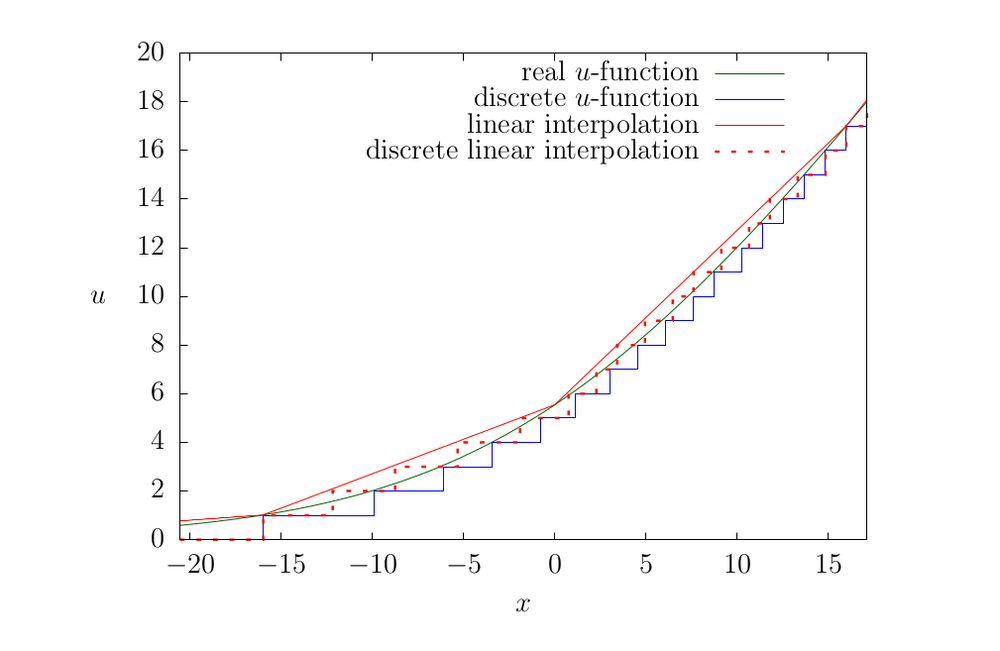
1. Есть идеальная вещественнозначная функция обновления, которая в точности задает модель экспоненциального распада (гладкая зеленая линия на графике).
2. Для практического применения ее приходится дискретизировать. Можно использовать представление с плавающей точкой (это, очевидно, тоже дискретизация, только не равномерная), а можно взять целочисленное. В данном случае применяется округление вниз, хотя это не принципиально (синяя линия).
3. Наконец, можно еще сильнее загрубить функцию обновления. В [1] для ускорения вычислений предлагалось вместо вычисления вещественнозначной функции с логарифмами и экспонентами использовать табличный подход. При этом предполагалось, что размер таблицы будет невелик, если используется малоразрядный счетчик. Однако ничто не мешает проредить таблицу, сократив ее размер еще в несколько раз, и реализовать линейную интерполяцию. Полученная функция обновления будет немного отличаться (красная пунктирная линия на графике).

Разумеется, в результате дискретизации функция обновления искажается, что само по себе не является проблемой, но приходится это учитывать при построении оценки интенсивности. Кроме того, неизбежно теряется строгая монотонность модели, вследствие чего снижается точность оценки. Степень искажения зависит от параметра \(\tau\) — чем он больше, тем ближе дискретизованная функция к исходной.

Ссылки

[1] Наша статья про распадную модель: https://habr.com/ru/company/qrator/blog/334354

[2] Экспоненциально взвешенное скользящее среднее: https://ru.wikipedia.org/wiki/Скользящая_средняя#Экспоненциально_взвешенное_скользящее_среднее

[3] Взвешенные скользящие средние: https://ru.wikipedia.org/wiki/Скользящая_средняя#Взвешенные_скользящие_средние

[4] Закон радиоактивного распада: https://ru.wikipedia.org/wiki/Закон_радиоактивного_распада

[5] Теорема Банаха о неподвижной точке: https://ru.wikipedia.org/wiki/Теорема_Банаха_о_неподвижной_точке

[6] Ayur Datar et al. — Maintaining Stream Statistics Over Sliding Windows — Society for Industrial and Applied Mathematics, Vol. 31, No. 6: http://www-cs-students.stanford.edu/~datar/papers/sicomp_streams.pdf

[7] Наша статья про счетчики Морриса: https://blog.qrator.net/ru/obzor-schyotchikov-morrisa_132/

[8] Трансляционная симметрия: https://ru.wikipedia.org/wiki/Трансляционная_симметрия