Мы рады представить вам заметку, написанную инженером Qrator Labs Дмитрием Камальдиновым. Если вы хотите быть частью нашей команды Core и заниматься подобными задачами - пишите нам на hr@qrator.net.
1 Введение
При реализации потоковых алгоритмов часто возникает задача подсчёта каких-то событий: приход пакета, установка соединения; при этом доступная память может стать узким местом: обычный \(n\)-битный счётчик позволяет учесть не более \(2^n - 1\) событий.
Одним из способов обработки большего диапазона значений, используя то же количество памяти, является вероятностный подсчёт. В этой статье будет предложен обзор известного алгоритма Морриса, а также некоторых его обобщений.
Другой способ уменьшить количество бит, необходимое для хранения значения счётчика, — использование распада. Об этом подходе мы рассказываем здесь, а также собираемся в ближайшее время опубликовать ещё одну заметку по теме.
Мы начнём с разбора простейшего алгоритма вероятностного подсчёта, выделим его недостатки (раздел 2). Затем (раздел 3) опишем алгоритм, впервые преложенный Робертом Моррисом в 1978 году, укажем его важнейшие свойства и приемущества. Для большинства нетривиальных формул и утверждений в тексте присутствуют наши доказательства — интересующийся читатель сможет найти их во вкладышах. В трёх последующих разделах мы изложим полезные расширения классического алгоритма: вы узнаете, что общего у счётчиков Морриса и экспоненциального распада, как можно уменьшить ошибку, пожертвовав максимальным значением, и как эффективно обрабатывать взвешенные события.
2 Вероятностный подсчёт, проблемы тривиального подхода
Основная идея вероятностного подсчёта — учёт очередного события с некоторой вероятностью. Рассмотрим сначала пример с постоянной вероятностью обновления:
\(\begin{equation*} C_{n+1} = \left\{\begin{array}{ll} C_n + 1 & \textit{с вероятностью $p = const$} \\ C_n & \textit{с вероятностью $1-p$.} \end{array}\right. \end{equation*}\)
Где через \(C_n\) обозначено значение счётчика после \(n\)-ой попытки обновления. Несложно понять, что \(C_n\) задаёт количество успехов среди \(n\) независимых испытаний Бернулли. Иначе говоря, \(C_n\) имеет биномиальное распределение:
\(\begin{align*} C_n \sim Bin(&n, p) \\ {\sf E} C_n = &np \\ {\sf D} C_n = &np(1-p). \end{align*}\)
В качестве оценки числа событий \(n\) естественно использовать \(\widehat{n}(C) := C/p\). Ясно, что такая оценка несмещённая: \({\sf E}\widehat{n}(C_n) = ({\sf E}C_n)/p = np/p = n\).
Описанный подход имеет несколько недостатков: во-первых, он позволяет учесть лишь в \(1/p = const\) раз больше событий по сравнению с простым инкрементальным счётчиком, чем заметно уступает счётчикам Морриса, как мы увидим далее. Во-вторых, относительная ошибка оценки велика при маленьких \(n\). Например, при \(n=1\) она вообще равна 100%. Оценить относительную ошибку можно с помощью коэффициента вариации:
\(\begin{align*} {\sf CV}\widehat{n}(C_n) = \frac{\sqrt{{\sf D}\widehat{n}(C_n)}}{{\sf E} \widehat{n}(C_n)} = \sqrt{\frac{1-p}{pn}}. \end{align*}\)
3 Счётчики Морриса
Счётчик Морриса обновляется с вероятностью, зависящей от текущего значения: первое обновление происходит с вероятностью 1, следующее с вероятностью 1/2, потом 1/4 и т.д.:
\(\begin{equation*} C_{n+1} = \left\{\begin{array}{ll} C_n + 1 & \textit{с вероятностью $2^{-C_n}$} \\ C_n & \textit{с вероятностью $1 - 2^{-C_n}$.} \end{array}\right. \end{equation*}\)
Как по значению счётчика оценить, сколько было событий? Обновление счётчика с \(x\) на \(x + 1\) происходит в среднем за \(2^x\) итераций, отсюда оценка числа событий \(\widehat{n}(C) := \sum_{i=0}^{C-1} 2^{i} = 2^C - 1\).
Важнейшими свойствами этой оценки являются
- её несмещённость, то есть значение оценки после \(n\) вероятностных обновлений в среднем равно \(n\),
Доказательство
\(\begin{align*} {\sf E}\left(2^{C_n} | C_{n-1} = y\right) =& \underbrace{2^{y + 1} 2^{-y}}_{\textit{счётчик обновился}} + \underbrace{2^y (1 - 2^{-y})}_{\textit{значение не изменилось}} = 2^y + 1 \implies \\ {\sf E}\left(2^{C_n}|C_{n-1}\right) =& 2^{C_{n-1}} + 1 \implies {\sf E}2^{C_n} = {\sf E}2^{C_{n-1}} + 1 = {\sf E}2^{C_{n-2}} + 2 = \dots \end{align*}\)
В самом начале значение счётчика равно 0: \(C_0 = 0\), тогда \({\sf E}2^{C_0} = 2^{0} = 1\), а значит \({\sf E} 2^{C_n} = \dots = n + 1\). Итого \({\sf E}\widehat{n}(C_n) = {\sf E}2^{C_n} - 1 = n\).
- а также независимость её относительной ошибки от \(n\).
Доказательство
Сначала посчитаем дисперсию \(\widehat{n}(C_n)\). Согласно известной формуле, \({\sf D}\widehat{n} = {\sf E}\widehat{n}^2 - ({\sf E}\widehat{n})^2\). Мы уже знаем, что \({\sf E}\widehat{n}(C_n) = n\). Осталось получить \({\sf E}\widehat{n}(C_n)^2\). Заметим, что
\( \begin{align*} {\sf E}\left(2^{C_n} - 1\right)^2 = {\sf E}2^{2C_n} - 2(n+1) + 1 = {\sf E}2^{2C_n} - 2n - 1. \end{align*}\)
Таким образом, остаётся узнать, чему равно \({\sf E}2^{2C_n}\).
\(\begin{align*} {\sf E}\left(2^{2C_n} | C_{n-1} = y\right) &= \underbrace{2^{2(y + 1)} 2^{-y}}_{\textit{счётчик обновился}} + \underbrace{2^{2y}(1 - 2^{-y})}_{\textit{значение не изменилось}} = \\ 3 \cdot 2^y +2^{2y} &\implies {\sf E}\left(2^{2C_n} | C_{n-1}\right) = 3 \cdot 2^{C_{n-1}} + 2^{2C_{n-1}} \implies \\ {\sf E} 2^{2C_n} = 3n &+ {\sf E}2^{2C_{n-1}} = 3n + 3(n-1) + {\sf E}2^{2C_{n-2}} = \dots = \sum_{i=1}^n 3i \end{align*}\)
Итого
\( \begin{equation*} {\sf D}\widehat{n}(C_n) = \frac{3n(n+1)}{2} - 2n - 1 - n^2 = \frac{n^2 - n - 2}{2} \end{equation*}\)
\(\begin{equation*} {} {\sf CV}\widehat{n}(C_n) = \frac{\sqrt{{\sf D}\widehat{n}(C_n)}}{{\sf E}\widehat{n}(C_n)} = \sqrt{\frac{n^2-n-2}{2n^2}} \sim \frac{1}{\sqrt{2}}. \end{equation*}\)
Таким образом, относительная ошибка оценки числа событий при использовании счётчика Морриса ограничена, примерно постоянна и почти не зависит от \(n\).
Оценить вероятность больших отклонений от среднего можно с помощью неравенства Чебышёва:
\(\begin{align*} {\sf P}(|\widehat{n}(C_n) - n| \ge \varepsilon n) \le \frac{{\sf D}\widehat{n}(C_n)}{\varepsilon^2n^2} \sim \frac{1}{2\varepsilon^2}. \end{align*}\)
- отметим здесь также, что покрываемый диапазон количества событий при использовании \({\bf X}\) бит памяти будет \(2^{2^{\bf X}} - 1\). Иначе говоря, для учёта \(n\) событий достаточно \(\mathcal{O}(\log \log n)\) бит памяти!
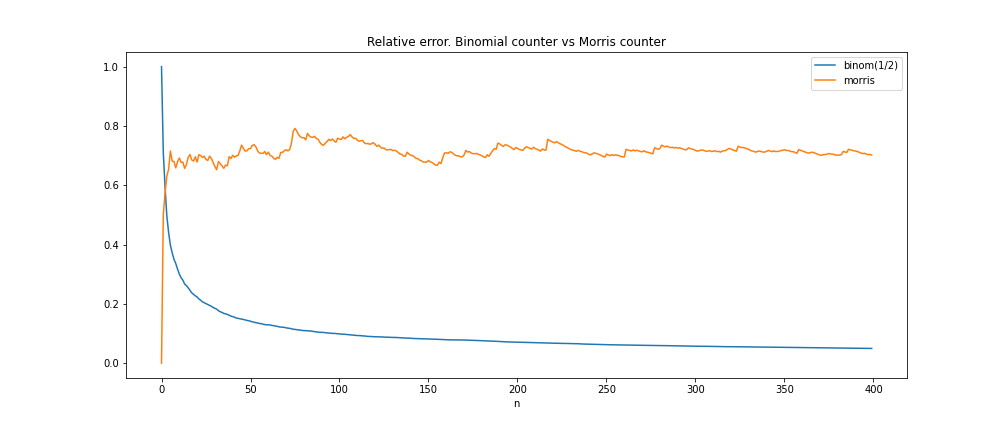
*для построения графика \(sample\_size=100\) раз запускался процесс обновления счётчика, затем каждой точке \(n\) сопоставлялось среднее значение по этой выборке относительной ошибки после \(n\) обновлений

4 Взвешенные обновления
Счётчики Морриса можно использовать для подсчёта взвешенных событий: например, для суммирования размеров приходящих пакетов. Простейший способ — обновление счётчика <вес события> раз — приводит к линейной по весу сложности обновления.

Заметим, что в каждый момент времени мы знаем, как распределено количество неудач до ближайшего изменения счётчика, — это геометрическое рапределение:
\(\begin{align*} {\sf P}(n_{fail} = k) = (1 - 2^{-C})^k 2^{-C} \implies n_{fail} \sim Geom(2^{-C}). \end{align*}\)
Учитывая этот факт, мы можем ускорить алгоритм, сразу пропуская все подряд идущие неудачные попытки обновления:

5 Распад
Часто возникает потребность учитывать самые новые события с большим весом. Например, при поиске интенсивных ключей в потоке интереснее понять, какой ключ интенсивен прямо сейчас, а не имеет высокую среднюю интенсивность за счёт своего бурного прошлого. В статье мы рассказывали о распадных счётчиках, спроектированных специально для решения этой задачи. Другой предпосылкой для некоего распада является то, что несмотря на суперэкономное использование памяти, когда-то и счётчик Морриса переполнится. Оказывается, счётчики Морриса тоже могут распадаться, причём очень похожим на EMA способом, но гораздо эффективнее.
Идея очень проста: будем периодически вычитать \(1\) из счётчика. Напомним, что значение \(C\) оценивает количество событий как \(\sum_{i=0}^{C-1} 2^i = 2^C - 1 =: n_0\). Соответственно, после вычитания \(1\) оценка станет \(2^{C-1} - 1 = \frac{1}{2}n_0 - \frac{1}{2}\). Иначе говоря, вычитание \(1\) уменьшает оценку в \(\sim 2\) раза! Мы можем добиться распада ровно в \(2\) раза, обновив с вероятностью \(\frac{1}{2}\) счётчик сразу после вычитания \(1\):

6 Мантисса и экспонента
Рассмотрим следующее обобщение счётчика Морриса: вероятность обновления уменьшается в \(2\) раза не на каждое успешное обновление, а на каждые \({\bf X}\). Возможной реализацией такого подхода будет разделение битов счётчика на две части: экспоненту, отвечающую за вероятность, и мантиссу, считающую количество успешных обновлений при текущей вероятности (чем-то похоже на представление чисел с плавающей точкой).

Рис. 2: разбиение битов счётчика на мантиссу (\({\bf M} = 5\) бит) и экспоненту (\({\bf E} = 3\) бит)
Введём обозначения для мантиссы и экспоненты:
\(\begin{align*} {\rm e}(C) &= C \gg {\bf M} \\ {\rm m}(C) &= C \& (2^{\bf M} - 1). \end{align*}\)
Теперь правило обновления и оценка числа событий записываются так:
\(\begin{align*} C_{n+1} &= \left\{\begin{array}{ll} C_n + 1, & \textit{с вероятностью $2^{-{\rm e}(C)}$} \\ C_n, & \textit{с вероятностью $1 - 2^{-{\rm e}(C)}$} \end{array}\right. \\ \widehat{n}(C) &= (2^{{\rm e}(C)} - 1)2^{\bf M} + 2^{{\rm e}(C)}{\rm m}(C). \end{align*}\)
Например, на рисунке 2 значение счётчика \(C = 89\), мантисса и экспонента равны \({\rm m} = 25\) и \({\rm e} = 2\) соответственно. А значит число событий оценивается как \(\widehat{n} = (2^2 - 1) \times 2^5 + 2^2 \times 25 = 196\).
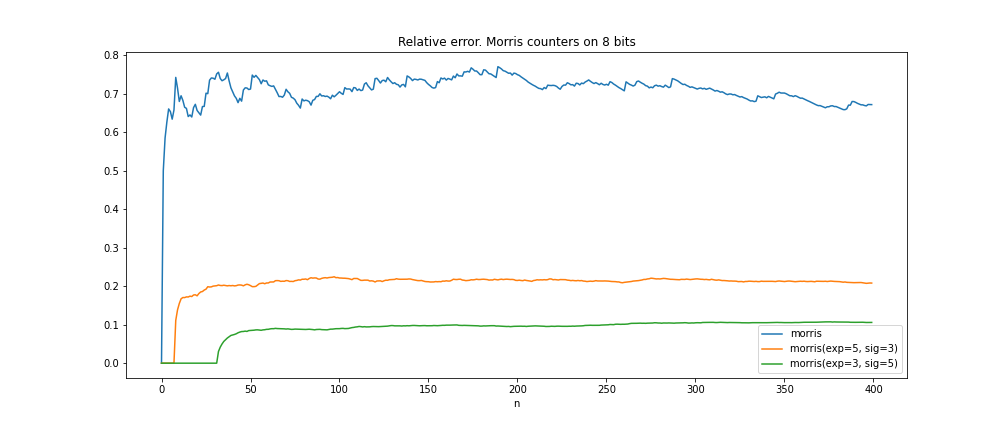
При таком разбиении биты экспоненты будут отвечать за покрываемый диапазон количества событий, а биты мантиссы за точность оценки (далее мы поясним подробнее, что это значит). Наилучшее распределение битов счётчика зависит от задачи; мы предлагаем отдавать как можно больше мантиссе, но чтобы экспоненциальных битов хватало для покрытия интересующего диапазона значений.
Описанный вариант счётчиков Морриса обладает следующими свойствами:
- покрываемый диапазон значений равен
\(\begin{align*} {\bf N}_{max} = 2^{2^{\bf E} + {\bf M}} - \left(2^{2^{\bf E} - 1} + 2^{\bf M}\right); \end{align*}\)
Доказательство
Покрываемый диапазон получить несложно, подставив в формулу для \(\widehat{n}\) максимальные возможные значения \({\rm m} = 2^{\bf M} - 1\) и \({\rm e} = 2^{\bf E} - 1\):
\(\begin{align*} {\bf N}_{max} = \left(2^{2^{\bf E} - 1} - 1\right)2^{\bf M} + 2^{2^{\bf E} - 1}\left(2^{\bf M} - 1\right) = 2^{2^{\bf E} + {\bf M}} - \left(2^{2^{\bf E} - 1} + 2^{\bf M}\right) \end{align*}\)
- новая оценка \(\widehat{n}\) также несмещённая: \({\sf E}\widehat{n}(C_n) = n\);
Доказательство
Аналогично доказательству утверждения для обычных счётчиков Морриса посчитаем условное мат.~ожидание \({\sf E}(C_n | C_{n - 1} = y)\). Причём сделаем это отдельно для \(y \equiv -1 \pmod{2^{\bf M}}\) (вероятность обновления изменится в случае успеха) и \(y \not\equiv -1 \pmod{2^{\bf M}}\).
\(\begin{align*} y \not\equiv -1 \pmod{2^{\bf M}} &\implies {\rm e}(y + 1) = {\rm e}(y), \quad {\rm m}(y + 1) = {\rm m}(y) + 1 \\ &\implies \widehat{n}(y + 1) = \widehat{n}(y) + 2^{{\rm e}(y)} \\ y \equiv -1 \pmod{2^{\bf M}} & \implies {\rm e}(y + 1) = {\rm e}(y) + 1,\\ &\phantom{\implies} \phantom{Z} {\rm m}(y) = 2^{\bf M} - 1, \quad {\rm m}(y + 1) = 0 \implies \\ \widehat{n}(y + 1) = \widehat{n}(y) &- 2^{{\rm e}(y)}\left(2^{\bf M} - 1\right) + 2^{{\rm e}(y) + {\bf M}} = \widehat{n}(y) + 2^{{\rm e}(y)} \end{align*}\)
В обоих случаях
\(\begin{align*} {\sf E}(2^{C_n} | C_{n-1} = y) &= \widehat{n}(y)\left(1 - 2^{-{\rm e}(y)}\right) + \left(\widehat{n}(y) + 2^{{\rm e}(y)}\right)2^{-{\rm e}(y)} = \widehat{n}(y) + 1. \end{align*}\)
- коэффициент вариации (и относительная ошибка) становятся ещё меньше! Мы не знаем его точное значение, но имеется такая оценка (сравните её с аналогичной для классического счётчика Морриса):
\(\begin{align*} {\sf CV}\widehat{n}(C_n) \le 2^{-\frac{{\bf M} + 1}{2}}. \end{align*}.\)

Алгоритмы взвешенных обновлений и распада тоже немного изменятся.
Аналогично подходу, описанному в разделе 4, чтобы эффективно выполнить взвешенное обновление, нужно понять, через сколько попыток обновления вероятность изменится. При отсутствии мантиссы вероятность меняется после каждого успешного обновления, теперь же после каждых \(2^{\bf M}\). А значит нам нужно распределение количества испытаний Бернулли (искомое число событий), среди которых ровно \(2^{\bf M}\) успешных. Такое распределение называется отрицательным биномиальным.
Замечание. Существует несколько определений отрицательного биномиального распределения. Будем придерживаться написанного в русскоязычной википедии, где сказано, что это распределение задаёт не общее число событий, а число неудач. Тогда чтобы получить число событий, нужно к случайной величине добавить количество успехов:
\(\begin{align*} n \sim \underbrace{ NegativeBinomial\left(2^{-{\rm e}(C)}, 2^{\bf M} - {\rm m}(C)\right)}_{\textit{неудач}} + \underbrace{\left(2^{\bf M} - {\rm m}(C)\right)}_{\textit{успехов}}. \end{align*}\)

Чтобы не генерировать отрицательное биномиальное распределение, можно загрубить алгоритм, всегда выбирая среднее этого распределения:

Чтобы выполнить распад, будем вычитать \(1\) из экспоненциальной части (иначе говоря, \(2^{\bf M}\) из значения счётчика). Тогда
\(\begin{align*} \widehat{n}(C - 2^{\bf M}) = (2^{{\rm e}(C) - 1} - 1)2^{\bf M} + 2^{{\rm e}(C) - 1}{\rm m}(C) = 1/2\widehat{n}(C) - 2^{{\bf M} - 1}. \end{align*}\)
Заметим, что при \({\bf M} > 0\) (а именно этот случай изучается в этом разделе) \(2^{{\bf M} - 1} \in \mathbb{N}\). Поэтому исправить оценку можно, вероятностно увеличив счётчик на \(2^{{\bf M} - 1}\):

7 Заключение
Счётчики Морриса — это очень круто! Пользуйтесь!
Последний раздел не содержит полезных на практике результатов, но...
8 Обобщённые вероятностные счётчики
В общем виде правило обновления счётчика определяется функцией вероятности \(F : C \mapsto [0, 1]\):
\(\begin{equation*} C_{n+1} = \left\{\begin{array}{ll} C_n + 1 & \textit{с вероятностью $F(C_n)$} \\ C_n & \textit{с вероятностью $1 - F(C_n)$.} \end{array}\right. \end{equation*}\)
В случае счётчиков Морриса \(F(C_n) = 2^{-C_n}\). При изучении вероятностных счётчиков мы попробовали взять линейную функцию вероятности: \(F(C_n) = 1 - \frac{C_n}{C_{max}}\) (\(C_{max}\) — некоторая константа, максимальное значение счётчика). Это привело к некоторым интересным результатам, которые будут кратко изложены в этом разделе.
Прежде чем представить эти результаты, напомним о двух математических сущностях.
Полный однородный симметрический многочлен степени \(n\) от \(m\) переменных \(x_1, \dots, x_m\) — это сумма всех возможных одночленов степени \(n\) от этих переменных с коэффициентами \(1\):
\(\begin{align*} \mathcal{H}_n(x_1, \dots x_m) = \sum_{\begin{array}{cc} & 0 \le i_j \le n \\ & i_1 + \dots + i_m = n \end{array}} x_1^{i_1} \cdots x_m^{i_m}. \end{align*}\)
Другая конструкция, которая нам понадобится, — число Стирлинга второго рода. Один из способов определить это число — комбинаторный: число Стирлинга второго рода \(\genfrac\{\}{0pt}{}{n}{m}\) — количество разбиений \(n\)-элементного множества на \(m\) непустых подмножеств. Числа Стирлинга связаны с полными симметрическим многочленами:
\(\begin{align*} \genfrac\{\}{0pt}{}{n+m}{m} = \mathcal{H}_m(1, 2, \dots, m). \end{align*}\)
С помощью \(\mathcal{H}\) можно записать в общем виде вероятность того, что после \(n\) попыток обновления значение счётчика равно \(m\):
\(\begin{align*} {\sf P}(C_n = m) = \left[\prod_{k=0}^{m-1} F(k) \right] \mathcal{H}_{n-m}(1-F(1), \dots 1-F(m)). \end{align*}\)
Эту формулу легко доказать по индукции, но также она несложно следует из простых комбинаторных рассуждений: фактически в ней записано, что для того, чтобы получить значение \(m\), нужны \(m\) успешных обновлений: с \(0\) до \(1\), с \(1\) до \(2\) и т.д., — за это отвечает множитель \(\prod_{k=0}^{m-1} F(k)\), и \(n - m\) неудачных, которые разбиваются на \(m\) групп: \(i_1\) неудачных обновлений с \(1\) до \(2\), \(i_2\) с \(2\) до \(3\) и т.д., что выражено \(\mathcal{H}_{n-m}\).
Наконец, при использовании линейной функции вероятности \(F(C) = 1 - \frac{C}{C_{max}}\) вероятность принимает вид
\(\begin{equation*} {\sf P}(C_n = m) = \genfrac\{\}{0pt}{}{n}{m}\frac{C_{max}!}{(C_{max} - m)!C_{max}^n}. \end{equation*}\)
Это и есть анонсированный выше интересный результат. Мы заметили число Стирлинга в значении вероятности достаточно случайно и до сих пор не знаем, можно ли обосновать его присутствие комбинаторынми рассуждениями (опираясь, на его комбинаторное определение). Другой вопрос — можно красиво записать аналогичную вероятность для счётчиков Морриса.
Математическое ожидание и дисперсия \(C_n\) (доказательства опускаем, но их несложно получить, используя формулу для \({\sf P}\) и свойства чисел Стирлинга).
\(\begin{align*} {\sf E}C_n &= C_{max}\left(1 - \left(1 - \frac{1}{C_{max}}\right)^n\right) \\ {\sf D}C_n &= C_{max}^2\left(\frac{1}{C_{max}}\left(1 - \frac{1}{C_{max}}\right)^n + \left(1 - \frac{1}{C_{max}}\right)\left(1 - \frac{2}{C_{max}}\right)^n - \left(1 - \frac{1}{C_{max}}\right)^{2n}\right). \end{align*}\)
Оценить число событий можно по методу моментов:
\(\begin{equation*} \widehat{n}_{MM} := \frac{\ln \left(1 - \frac{C_n}{C_{max}}\right)}{\ln \left(1 - \frac{1}{C_{max}}\right)} \end{equation*}\)
или аналогично счётчикам Морриса, учитывая, что \(1 + 1/2 + \dots + 1/n \sim \ln n\):
\(\begin{equation*} \widehat{n} := C_{max}\ln \left(\frac{1}{1 - \frac{C_n}{C_{max}}}\right). \end{equation*}\)
Список литературы
[1] Morris, R.Counting large numbers of events in small registersCommunications of the ACM, 1978 21(10), 840-842.
[2] http://gregorygundersen.com/blog/2019/11/11/morris-algorithm/ − хороший обзор счётчиков Морриса на английском языке
[3] https://habr.com/ru/company/qrator/blog/334354/ − наша статья про EMA-счётчики
[4] https://habr.com/ru/post/208268/ − сторонний материал про счётчики Морриса
